Bài 8 trang 116 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Cánh Diều, tập trung vào việc ôn tập chương 4: Hàm số lượng giác và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số lượng giác, các phép biến đổi lượng giác và đồ thị hàm số để giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Hình 101 là hình chụp đền Kukulcan, là một kim tự tháp Trung Mỹ nằm ở khu di tích Chichen Itza
Đề bài
Hình 101 là hình chụp đền Kukulcan, là một kim tự tháp Trung Mỹ nằm ở khu di tích Chichen Itza, Mexico, được người Maya xây vào khoảng từ thế kỉ IX đến thế kỉ XII. Phần thân của đền, không bao gồm ngôi đền nằm phía trên, có dạng một khối chóp cụt tứ giác đều (không tính cầu thang và coi các mặt bên là phẳng) với độ dài đáy dưới là 55,3 m, chiều cao là 24 m, góc giữa cạnh bên và mặt phẳng đáy là khoảng \({47^ \circ }\).

(Nguồn: https://vi.wikipedia.org)
Tính thể tích phần thân ngôi đền có dạng khối chóp cụt tứ giác đều đó theo đơn vị mét khối (làm tròn kết quả đến hàng phần trăm).
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right)\).
Lời giải chi tiết
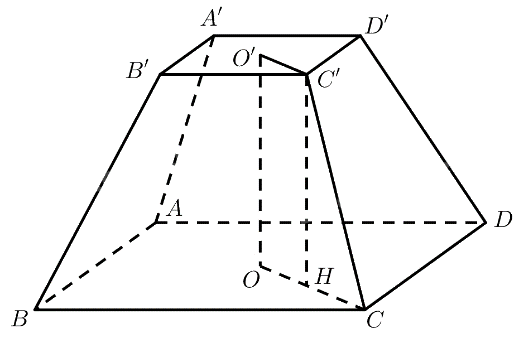
Mô hình hoá phần thân của đền bằng cụt chóp tứ giác đều \(ABCD.A'B'C'D'\) với \(O,O'\) là tâm của hai đáy. Vậy \(AB = 55,3;OO' = 24;\left( {CC',\left( {ABCD} \right)} \right) = {47^ \circ }\)
\(ABCD\) là hình vuông
\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = 55,3\sqrt 2 \Rightarrow CO = \frac{1}{2}AC = 27,65\sqrt 2 \)
Kẻ \(C'H \bot OC\left( {H \in OC} \right) \Rightarrow C'H\parallel OO' \Rightarrow C'H \bot \left( {ABCD} \right)\)
\( \Rightarrow \left( {CC',\left( {ABCD} \right)} \right) = \left( {CC',CH} \right) = \widehat {HCC'} = {47^ \circ }\)
\(OHC'O'\) là hình chữ nhật \( \Rightarrow OO' = C'H = 24,CH = O'C'\)
\(\Delta CC'H\) vuông tại \(H \Rightarrow CH = \frac{{C'H}}{{\tan \widehat {HCC'}}} = \frac{{24}}{{\tan {{47}^ \circ }}} \approx 22,38\)
\(O'C' = OH = CO - CH \approx 16,72 \Rightarrow A'C' = 2O'C' = 33,44\)
\(A'B'C'D'\) là hình vuông \( \Rightarrow A'B' = \frac{{A'C'}}{{\sqrt 2 }} \approx 23,65\)
Diện tích đáy lớn là: \(S = A{B^2} = 55,{3^2} = 3058,09\left( {{m^2}} \right)\)
Diện tích đáy bé là: \(S' = A'B{'^2} = 23,{65^2} = 559,3225\left( {{m^2}} \right)\)
Thể tích hình chóp cụt là:
\(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right)\)
\(= \frac{1}{3}.24\left( {3058,09 + \sqrt {3058,09.559,3225} + 559,3225} \right)\)
\(\approx 39402,06\left( {{m^3}} \right)\)
Vậy thể tích phần thân ngôi đền có dạng khối chóp cụt tứ giác đều đó là \(39402,06\left( {{m^3}} \right)\)
Bài 8 trang 116 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về hàm số lượng giác và ứng dụng của chúng. Dưới đây là lời giải chi tiết cho từng phần của bài tập này:
Phương trình a: sin(x) = 1/2
Để giải phương trình này, ta cần tìm các giá trị của x sao cho sin(x) = 1/2. Ta biết rằng sin(π/6) = 1/2. Do đó, nghiệm tổng quát của phương trình là:
Phương trình b: cos(x) = -√3/2
Tương tự, ta tìm các giá trị của x sao cho cos(x) = -√3/2. Ta biết rằng cos(5π/6) = -√3/2. Do đó, nghiệm tổng quát của phương trình là:
Phương trình c: tan(x) = 1
Để giải phương trình này, ta tìm các giá trị của x sao cho tan(x) = 1. Ta biết rằng tan(π/4) = 1. Do đó, nghiệm tổng quát của phương trình là:
Bất phương trình a: sin(x) > 1/2
Để giải bất phương trình này, ta cần tìm các khoảng giá trị của x sao cho sin(x) > 1/2. Dựa vào đường tròn lượng giác, ta thấy rằng sin(x) > 1/2 khi π/6 < x < 5π/6. Do đó, tập nghiệm của bất phương trình là:
Bất phương trình b: cos(x) ≤ -1/2
Tương tự, ta tìm các khoảng giá trị của x sao cho cos(x) ≤ -1/2. Dựa vào đường tròn lượng giác, ta thấy rằng cos(x) ≤ -1/2 khi 2π/3 ≤ x ≤ 4π/3. Do đó, tập nghiệm của bất phương trình là:
Các phương trình lượng giác nâng cao thường đòi hỏi việc sử dụng các công thức biến đổi lượng giác và kỹ năng giải phương trình phức tạp hơn. Ví dụ, phương trình 2sin(x)cos(x) = 1 có thể được giải bằng cách sử dụng công thức sin(2x) = 2sin(x)cos(x). Khi đó, phương trình trở thành sin(2x) = 1, và nghiệm tổng quát là:
Lưu ý: Khi giải các phương trình và bất phương trình lượng giác, cần chú ý đến điều kiện xác định của hàm số lượng giác và kiểm tra lại nghiệm để đảm bảo tính chính xác.
Hy vọng lời giải chi tiết này sẽ giúp các bạn học sinh hiểu rõ hơn về Bài 8 trang 116 SGK Toán 11 tập 2 - Cánh Diều và tự tin giải các bài tập tương tự.