Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết các bài tập trong mục 2 trang 62 SGK Toán 11 tập 2 - Cánh Diều.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho hàm số y = f(x) có đồ thị (C), một điểm ({M_0}) cố định thuộc (C) có hoành độ ({x_0}).
Cho hàm số y = f(x) có đồ thị (C), một điểm \({M_0}\) cố định thuộc (C) có hoành độ \({x_0}\). Với mỗi điểm M thuộc (C) khác \({M_0}\), kí hiệu \({x_M}\) là hoành độ của điểm M và \({k_M}\) là hệ số góc của cát tuyến \({M_0}M\). Giả sử tồn tại giới hạn hữu hạn \({k_0} = \mathop {\lim }\limits_{{x_M} \to {x_0}} {k_M}\). Khi đó, ta coi đường thẳng \({M_0}T\) đi qua \({M_0}\) và có hệ số góc là \({k_0}\) là ví trị giới hạn của cát tuyến \({M_0}M\) khi điểm M di chuyển dọc theo (C) dần tới \({M_0}\) . Đường thẳng \({M_0}T\)được gọi là tiếp tuyến của (C) tại điểm \({M_0}\), còn \({M_0}\) được gọi là tiếp điểm (Hình 3).
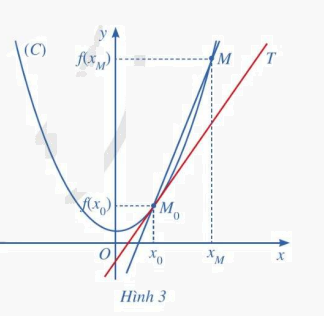
a) Xác định hệ số góc \({k_0}\) của tiếp tuyến \({M_0}T\) theo \({x_0}\)
b) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm \({M_0}\)
Phương pháp giải:
Áp dụng định nghĩa đạo hàm để làm bài
Lời giải chi tiết:
a) \({k_0} = \mathop {\lim }\limits_{x \to {x_M}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}} = f'({x_0})\)
b) Phương tình tiếp tuyến của đồ thị hàm số tại điểm \({M_0}\):
\(y = {k_0}(x - {x_0}) + {y_0}\)
Viết phương trình tiếp tuyến của đồ thị hàm số \(y = \frac{1}{x}\) tại điểm N (1; 1)
Phương pháp giải:
Dựa vào ví dụ 3 để làm
Lời giải chi tiết:
- Tiếp tuyến của đồ thị tại điểm có hoành độ bằng 1 có hệ số góc là:
\(f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{x} - 1}}{{x - 1}} = - 1\)
- Phương trình tiếp tuyến của đồ thị tại điểm N(1; 1) là:
\(y = - 1.\left( {x - 1} \right) + 1 = - x + 1 + 1 = - x + 2\) \(\)
Mục 2 trang 62 SGK Toán 11 tập 2 - Cánh Diều tập trung vào việc ôn tập chương 3: Hàm số lượng giác và ứng dụng của hàm số lượng giác. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức về đồ thị hàm số lượng giác, phương trình lượng giác, và các ứng dụng thực tế của hàm số lượng giác để giải quyết các bài toán cụ thể.
Mục 2 bao gồm các bài tập trắc nghiệm và tự luận, được chia thành các dạng bài khác nhau. Dưới đây là phân tích chi tiết về nội dung và phương pháp giải từng dạng bài:
Các bài tập trắc nghiệm này thường yêu cầu học sinh xác định các yếu tố của đồ thị hàm số lượng giác như biên độ, chu kỳ, pha ban đầu, và các điểm đặc biệt trên đồ thị. Để giải quyết các bài tập này, học sinh cần nắm vững các kiến thức về đồ thị hàm số lượng giác và khả năng đọc hiểu đồ thị.
Các bài tập tự luận về phương trình lượng giác thường yêu cầu học sinh giải các phương trình lượng giác cơ bản và các phương trình lượng giác phức tạp hơn. Để giải quyết các bài tập này, học sinh cần nắm vững các công thức lượng giác, các phương pháp giải phương trình lượng giác, và khả năng biến đổi phương trình.
Ví dụ: Giải phương trình sin(x) = 1/2.
Lời giải: Phương trình có các nghiệm x = π/6 + k2π và x = 5π/6 + k2π, với k là số nguyên.
Các bài tập ứng dụng của hàm số lượng giác thường yêu cầu học sinh vận dụng kiến thức về hàm số lượng giác để giải quyết các bài toán thực tế như bài toán về dao động điều hòa, bài toán về đo đạc, và bài toán về vật lý.
Ví dụ: Một vật dao động điều hòa với phương trình x = 5cos(2πt + π/3). Xác định biên độ và chu kỳ của dao động.
Lời giải: Biên độ của dao động là 5 và chu kỳ của dao động là T = 1/f = 1/(π/2) = 2/π.
| Công thức | Mô tả |
|---|---|
| sin2(x) + cos2(x) = 1 | Công thức lượng giác cơ bản |
| tan(x) = sin(x) / cos(x) | Công thức tính tan(x) |
| cot(x) = cos(x) / sin(x) | Công thức tính cot(x) |
Hy vọng rằng với những hướng dẫn chi tiết và phương pháp giải bài tập hiệu quả trên đây, bạn sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 62 SGK Toán 11 tập 2 - Cánh Diều. Chúc bạn học tập tốt!