Bài 13 trang 56 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Cánh Diều, tập trung vào các kiến thức về đạo hàm của hàm số. Bài tập này yêu cầu học sinh vận dụng các công thức và quy tắc đạo hàm đã học để giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập một cách hiệu quả.
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số mũ (y = {a^x};,y = {b^x};,y = {c^x}) được cho bởi Hình 14
Đề bài
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số mũ \(y = {a^x};\,y = {b^x};\,y = {c^x}\) được cho bởi Hình 14. Kết luận nào sau đây là đúng đối với ba số a, b, c ?
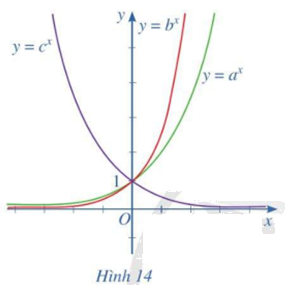
A. c < a < b
B. c < b < a
C. a < b < c
D. b < c < a
Phương pháp giải - Xem chi tiết
Dựa vào các hệ số và tính đồng biến, nghịch biến của hàm số mũ để suy ra
Lời giải chi tiết
- Do \({c^x}\) nghịch biến, \({a^x},{b^x}\) đồng biến => c < 1, a > 1, b > 1 => c nhỏ nhất => loại C, D
- Dựa vào đồ thị ta thấy, \({b^x}\) có đồ thị đi lên cao hơn so với \({a^x}\) => b > a => Chọn A
Bài 13 trang 56 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài 13 yêu cầu học sinh tính đạo hàm của các hàm số sau:
1. Giải f(x) = x3 - 3x2 + 2x - 5
Áp dụng quy tắc đạo hàm của tổng và hiệu, ta có:
f'(x) = 3x2 - 6x + 2
2. Giải g(x) = (x2 + 1)(x - 2)
Áp dụng quy tắc đạo hàm của tích, ta có:
g'(x) = (2x)(x - 2) + (x2 + 1)(1) = 2x2 - 4x + x2 + 1 = 3x2 - 4x + 1
3. Giải h(x) = sin(2x) + cos(x)
Áp dụng quy tắc đạo hàm của tổng và các hàm lượng giác, ta có:
h'(x) = cos(2x) * 2 - sin(x) = 2cos(2x) - sin(x)
4. Giải k(x) = ex + ln(x)
Áp dụng quy tắc đạo hàm của tổng và các hàm mũ, logarit, ta có:
k'(x) = ex + 1/x
Để hiểu sâu hơn về đạo hàm, bạn có thể tham khảo thêm các tài liệu sau:
Đạo hàm là một khái niệm quan trọng trong toán học, có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau như vật lý, kinh tế, kỹ thuật. Việc nắm vững kiến thức về đạo hàm sẽ giúp bạn giải quyết các bài toán thực tế một cách hiệu quả.
Giả sử chúng ta có hàm số y = x4 + 2x2 - 1. Để tính đạo hàm của hàm số này, ta áp dụng quy tắc đạo hàm của tổng và lũy thừa:
y' = 4x3 + 4x
Ví dụ này cho thấy việc áp dụng đúng quy tắc đạo hàm là rất quan trọng để có được kết quả chính xác.
Để rèn luyện kỹ năng giải bài tập về đạo hàm, bạn có thể thử giải các bài tập sau:
Hy vọng với lời giải chi tiết và hướng dẫn trên, bạn đã hiểu rõ cách giải Bài 13 trang 56 SGK Toán 11 tập 2 - Cánh Diều. Chúc bạn học tập tốt!