Giải Bài 2 trang 104 SGK Toán 11 tập 1 - Cánh Diều

Bài 2 trang 104 SGK Toán 11 tập 1 - Cánh Diều

Bài 2 trang 104 SGK Toán 11 tập 1 - Cánh Diều: Giải pháp chi tiết và dễ hiểu

Bài 2 trang 104 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn của hàm số để giải quyết các bài toán cụ thể.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 2 trang 104 SGK Toán 11 tập 1 - Cánh Diều, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Trong Hình 57, khi cắt bánh sinh nhật, mặt cắt và mặt khay đựng bánh lần lượt gợi nên hình ảnh mặt phẳng (Q) và mặt phẳng (P)

Đề bài

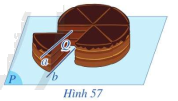
Trong Hình 57, khi cắt bánh sinh nhật, mặt cắt và mặt khay đựng bánh lần lượt gợi nên hình ảnh mặt phẳng (Q) và mặt phẳng (P); mép trên và mép dưới của lát cắt lần lượt gợi nên hình ảnh hai đường thẳng a và b trong đó a song song với mặt phẳng (P). Cho biết hai đường thẳng a, b có song song với nhau hay không.

Bài 2 trang 104 SGK Toán 11 tập 1 - Cánh Diều 1

Phương pháp giải - Xem chi tiết Bài 2 trang 104 SGK Toán 11 tập 1 - Cánh Diều 2

Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng cũng song song với đường thẳng đó.

Lời giải chi tiết

Hai đường thẳng a, b song song với nhau vì a song song với (P) mà (Q) cắt (P) tại giao tuyến b.

Tức là,

\(\left\{ \begin{array}{l}a \subset (Q)\\a//(P)\\(Q) \cap (P) = b\end{array} \right. \Rightarrow a//b\)

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Bài 2 trang 104 SGK Toán 11 tập 1 - Cánh Diều – hành trang không thể thiếu trong chuyên mục Giải bài tập Toán 11 trên nền tảng toán math. Bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Bài 2 trang 104 SGK Toán 11 tập 1 - Cánh Diều: Giải chi tiết và phân tích chuyên sâu

Bài 2 trang 104 SGK Toán 11 tập 1 - Cánh Diều thuộc chương trình học về giới hạn của hàm số. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản về giới hạn, các tính chất của giới hạn và các phương pháp tính giới hạn.

Nội dung bài tập

Bài 2 yêu cầu học sinh tính giới hạn của các hàm số khi x tiến tới một giá trị cụ thể. Các hàm số có thể là hàm đa thức, hàm phân thức, hàm lượng giác hoặc các hàm số khác.

Phương pháp giải

Có nhiều phương pháp để tính giới hạn của hàm số, tùy thuộc vào dạng của hàm số. Một số phương pháp phổ biến bao gồm:

Phương pháp trực tiếp: Thay trực tiếp giá trị của x vào hàm số để tính giới hạn. Phương pháp này chỉ áp dụng được khi hàm số xác định tại giá trị x đó.
Phương pháp phân tích thành nhân tử: Phân tích tử số và mẫu số thành nhân tử để rút gọn biểu thức và loại bỏ các yếu tố gây khó khăn cho việc tính giới hạn.
Phương pháp nhân liên hợp: Nhân tử số và mẫu số với liên hợp của biểu thức để loại bỏ các yếu tố gây khó khăn cho việc tính giới hạn.
Phương pháp sử dụng định lý giới hạn: Áp dụng các định lý giới hạn để tính giới hạn của các hàm số phức tạp.

Giải chi tiết Bài 2 trang 104 SGK Toán 11 tập 1 - Cánh Diều

Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi trong Bài 2 trang 104 SGK Toán 11 tập 1 - Cánh Diều.

Câu a: Tính lim_x→2 (x² - 4) / (x - 2)

Lời giải:

Phân tích tử số thành nhân tử: x² - 4 = (x - 2)(x + 2)
Rút gọn biểu thức: (x² - 4) / (x - 2) = (x - 2)(x + 2) / (x - 2) = x + 2
Tính giới hạn: lim_x→2 (x + 2) = 2 + 2 = 4

Vậy, lim_x→2 (x² - 4) / (x - 2) = 4

Câu b: Tính lim_x→3 (x³ - 27) / (x - 3)

Lời giải:

Phân tích tử số thành nhân tử: x³ - 27 = (x - 3)(x² + 3x + 9)
Rút gọn biểu thức: (x³ - 27) / (x - 3) = (x - 3)(x² + 3x + 9) / (x - 3) = x² + 3x + 9
Tính giới hạn: lim_x→3 (x² + 3x + 9) = 3² + 3*3 + 9 = 9 + 9 + 9 = 27

Vậy, lim_x→3 (x³ - 27) / (x - 3) = 27

Lưu ý khi giải bài tập về giới hạn

Khi giải bài tập về giới hạn, học sinh cần lưu ý một số điều sau:

Kiểm tra xem hàm số có xác định tại giá trị x hay không.
Chọn phương pháp giải phù hợp với dạng của hàm số.
Rút gọn biểu thức trước khi tính giới hạn.
Sử dụng các định lý giới hạn một cách chính xác.

Ứng dụng của giới hạn trong thực tế

Giới hạn là một khái niệm quan trọng trong toán học và có nhiều ứng dụng trong thực tế, chẳng hạn như:

Tính vận tốc tức thời của một vật chuyển động.
Tính đạo hàm của một hàm số.
Tính diện tích dưới đường cong.

Hy vọng rằng lời giải chi tiết và phân tích chuyên sâu về Bài 2 trang 104 SGK Toán 11 tập 1 - Cánh Diều sẽ giúp học sinh hiểu rõ hơn về khái niệm giới hạn và tự tin giải các bài tập tương tự.