Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 75, 76 SGK Toán 11 tập 1 - Cánh Diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Mục tiêu của chúng tôi là hỗ trợ các em học tập hiệu quả, tiết kiệm thời gian và đạt kết quả cao trong môn Toán.
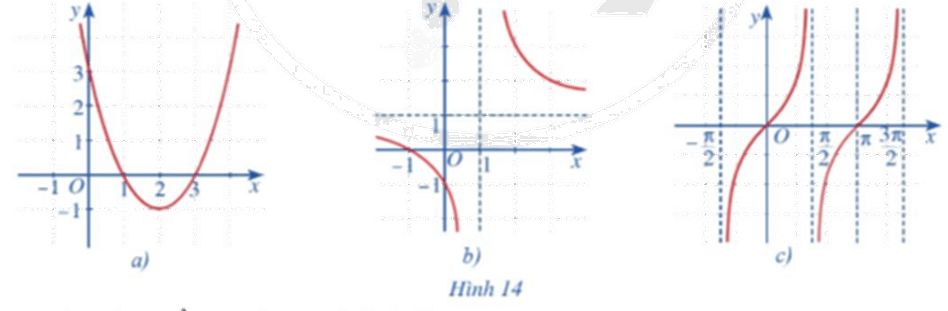
Quan sát đồ thị các hàm số: \(y = {x^2} - 4x + 3\) (Hình 14a); \(y = \frac{{x + 1}}{{x - 1}}\,\,\left( {x \ne 1} \right)\) (Hình 14b); \(y = \tan x\) (Hình 14c) và nêu nhận xét về tính liên tục của mỗi hàm số đó trên từng khoảng của tập xác định.
Quan sát đồ thị các hàm số: \(y = {x^2} - 4x + 3\) (Hình 14a);
\(y = \frac{{x + 1}}{{x - 1}}\,\,\left( {x \ne 1} \right)\) (Hình 14b);
\(y = \tan x\) (Hình 14c).
Và nêu nhận xét về tính liên tục của mỗi hàm số đó trên từng khoảng của tập xác định.
Phương pháp giải:
Đồ thị hàm số liên tục trên một khoảng là “đường liền” trên khoảng đó.
Lời giải chi tiết:
Hình 14a đồ thị là đường cong Parabol liền mạch nên hàm số liên tục trên toàn bộ trên khoảng xác định.
Hình 14b đồ thị bị chia làm hai nhánh:
- Với x < 1 ta thấy hàm số là một đường cong liền nên liên tục.
- Với x > 1 ta thấy hàm số là một đường cong liền nên liên tục.
Vậy hàm số liên tục trên từng khoảng xác định.
Hình 14c đồ thị hàm số y = tanx chia thành nhiều nhánh, và mỗi nhánh là các đường cong liền. Do đó hàm số liên tục trên mỗi khoảng xác định của chúng.
Hàm số \(f\left( x \right) = \frac{{x + 2}}{{x - 8}}\) có liên tục trên mỗi khoảng \(\left( { - \infty ;8} \right),\left( {8; + \infty } \right)\) hay không?
Phương pháp giải:
Hàm phân thức hữu tỉ liên tục trên từng khoảng xác định của chúng.
Lời giải chi tiết:
Do \(f\left( x \right) = \frac{{x + 2}}{{x - 8}}\) là hàm phân thức hữu tỉ xác định khi \(x \ne 8\) nên hàm số đó liên tục trên mỗi khoảng \(\left( { - \infty ;8} \right),\left( {8; + \infty } \right)\)
Cho hai hàm số \(f\left( x \right) = {x^3} + x\) và \(g\left( x \right) = {x^2} + 1\,\,\left( {x \in \mathbb{R}} \right).\) Hãy cho biết:
a) Hai hàm số \(f\left( x \right),g\left( x \right)\) có liên tục tại \(x = 2\) hay không.
b) Các hàm số \(f\left( x \right) + g\left( x \right);f\left( x \right) - g\left( x \right);f\left( x \right).g\left( x \right);\frac{{f\left( x \right)}}{{g\left( x \right)}}\) có liên tục tại \(x = 2\) hay không.
Phương pháp giải:
Các hàm đa thức liên tục trên \(\mathbb{R}\)
Lời giải chi tiết:
a) Ta có \(f\left( x \right),g\left( x \right)\) là các hàm đa thức nên các hàm số \(f\left( x \right),g\left( x \right)\) liên tục trên \(\mathbb{R}\)
Vậy các hàm số \(f\left( x \right),g\left( x \right)\) liên tục tại \(x = 2\)
b) \(\begin{array}{l}f\left( x \right) + g\left( x \right) = {x^3} + {x^2} + x + 1\\f\left( x \right) - g\left( x \right) = {x^3} - {x^2} + x - 1\\f\left( x \right).g\left( x \right) = \left( {{x^3} + x} \right)\left( {{x^2} + 1} \right) = {x^5} + 2{x^3} + x\\\frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{{x^3} + x}}{{{x^2} + 1}} = \frac{{x\left( {{x^2} + 1} \right)}}{{{x^2} + 1}} = x\end{array}\)
Ta có \(f\left( x \right) + g\left( x \right);f\left( x \right) - g\left( x \right);f\left( x \right).g\left( x \right);\frac{{f\left( x \right)}}{{g\left( x \right)}}\) là các hàm đa thức nên các hàm số \(f\left( x \right),g\left( x \right)\) liên tục trên \(\mathbb{R}\)
Vậy các hàm số \(f\left( x \right) + g\left( x \right);f\left( x \right) - g\left( x \right);f\left( x \right).g\left( x \right);\frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục tại \(x = 2\)
Xét tính liên tục của hàm số \(f\left( x \right) = \sin x + \cos x\) trên \(\mathbb{R}.\)
Phương pháp giải:
- Hàm số lượng giác \(y = \sin x,y = \cos x\) liên tục trên \(\mathbb{R}.\)
- Định lí tính liên tục của tổng của hai hàm số liên tục:
Giả sử hai hàm số \(y = f(x)\) và \(y = g(x)\) liên tục tại điểm \({x_0}\). Khi đó các hàm số \(y = f(x) \pm g(x)\)và \(y = f(x).g(x)\) liên tục tại điểm \({x_0}\).
Lời giải chi tiết:
Vì hai làm lượng giác \(y = \sin x,y = \cos x\) liên tục trên \(\mathbb{R}\)
\( \Rightarrow f\left( x \right) = \sin x + \cos x\) liên tục trên \(\mathbb{R}\)
Mục 2 của chương trình Toán 11 tập 1 - Cánh Diều tập trung vào các kiến thức về phép biến hình. Cụ thể, các em sẽ được làm quen với các phép biến hình cơ bản như phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các kiến thức này là nền tảng quan trọng để giải quyết các bài toán hình học trong chương trình học.
Bài tập mục 2 trang 75, 76 SGK Toán 11 tập 1 - Cánh Diều bao gồm các dạng bài tập khác nhau, yêu cầu học sinh vận dụng kiến thức về các phép biến hình để giải quyết các vấn đề cụ thể. Dưới đây là một số dạng bài tập chính:
Để giúp các em giải quyết các bài tập một cách hiệu quả, giaitoan.edu.vn cung cấp lời giải chi tiết cho từng bài tập trong mục 2 trang 75, 76 SGK Toán 11 tập 1 - Cánh Diều. Các lời giải này được trình bày một cách rõ ràng, dễ hiểu, kèm theo các hình vẽ minh họa để giúp các em hình dung rõ hơn về bài toán.
Đề bài: Cho điểm A(1; 2). Tìm ảnh A' của điểm A qua phép tịnh tiến theo vectơ v = (3; -1).
Lời giải:
Gọi A'(x'; y') là ảnh của điểm A qua phép tịnh tiến theo vectơ v. Khi đó, ta có:
x' = x + vx = 1 + 3 = 4
y' = y + vy = 2 + (-1) = 1
Vậy, A'(4; 1).
Để giải các bài tập về phép biến hình một cách hiệu quả, các em nên lưu ý một số mẹo sau:
Ngoài SGK Toán 11 tập 1 - Cánh Diều, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức về phép biến hình:
Hy vọng rằng, với lời giải chi tiết và các hướng dẫn hữu ích trên đây, các em sẽ tự tin giải quyết các bài tập mục 2 trang 75, 76 SGK Toán 11 tập 1 - Cánh Diều. Chúc các em học tập tốt!