Bài 2 trang 14 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Cánh Diều, tập trung vào việc vận dụng kiến thức về hàm số và đồ thị để giải các bài toán thực tế. Bài tập này đòi hỏi học sinh phải nắm vững các khái niệm cơ bản và kỹ năng giải toán liên quan.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Mẫu số liệu ghi lại cân nặng của 30 học sinh (đơn vị: kilogam):
Đề bài
Mẫu số liệu ghi lại cân nặng của 30 học sinh (đơn vị: kilogam):

a) Lập bảng tần số ghép nhóm cho mẫu số liệu trên có tám nhóm ứng với tám nửa khoảng:
[15 ; 20), [20 ; 25), [25 ; 30), [30 ; 35), [35 ; 40), [40 ; 45), [45 ; 50), [50 ; 55)
b) Xác định số trung bình cộng, trung vị, tứ phân vị của mẫu số liệu ghép nhóm trên.
c) Mốt của mẫu số liệu ghép nhóm trên là bao nhiêu?
Phương pháp giải - Xem chi tiết
- Lần lượt đếm số lượng của từng nhóm để lập bảng
- Áp dụng các công thức vừa được học để xác định các đại lượng tiêu biểu
Lời giải chi tiết
a) Bảng tần số ghép nhóm cho mẫu số liệu trên có tám nhóm ứng với tám nửa khoảng:
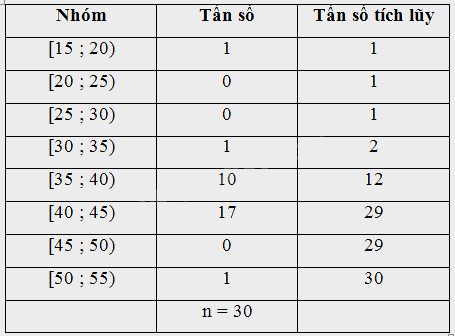
b) Các đại lượng tiêu biểu:
- Trung bình cộng: \(\overline x = \frac{{17,5.1+ 22,5.0 + 27,5.0 + 32,5.1 + 37,5.10 + 42,5.17 + 47,5.0 + 52,5.1}}{{30}} = 40\)
- Trung vị: \({M_e} = r + \left( {\frac{{\frac{n}{2} - c{f_{k - 1}}}}{{{n_k}}}} \right).d = 40 + \left( {\frac{{15 - 12}}{{17}}} \right).5 = 40,88\)
- Tứ phân vị:
+ Tứ phân vị thứ hai \({Q_2} = {M_e} = 40,88\)
+ Tứ phân vị thứ nhất: \({Q_1} = s + \left( {\frac{{\frac{n}{4} - c{f_{p - 1}}}}{{{n_p}}}} \right).h = 35 + \left( {\frac{{7,5 - 2}}{{10}}} \right).5 = 37,75\)
+ Tứ phân vị thứ ba: \(Q = t + \left( {\frac{{\frac{{3n}}{4} - c{f_{q - 1}}}}{{{n_q}}}} \right).l = 40 + \left( {\frac{{22,5 - 12}}{{17}}} \right).5 = 43,09\)
c) Mốt của mẫu số liệu:\({M_o} = u + \left( {\frac{{{n_i} - {n_{i - 1}}}}{{2{n_i} - {n_{i - 1}} - {n_{i + 1}}}}} \right).g = 40 + \left( {\frac{{17 - 10}}{{2.17 - 10 - 0}}} \right).5= 41,46\)
Bài 2 trang 14 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về hàm số bậc hai và ứng dụng của nó trong việc giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như tập xác định, tập giá trị, điểm cực trị, và cách vẽ đồ thị hàm số.
Bài 2 yêu cầu học sinh xét hàm số f(x) = x2 - 4x + 3 và thực hiện các yêu cầu sau:
1. Xác định tập xác định:
Hàm số f(x) = x2 - 4x + 3 là một hàm số bậc hai, có tập xác định là tập số thực, tức là D = ℝ.
2. Tìm tọa độ đỉnh của parabol:
Tọa độ đỉnh của parabol có dạng (x0; y0), trong đó x0 = -b / 2a và y0 = f(x0). Trong trường hợp này, a = 1 và b = -4, do đó:
Vậy tọa độ đỉnh của parabol là (2; -1).
3. Tìm trục đối xứng của parabol:
Trục đối xứng của parabol là đường thẳng x = x0, tức là x = 2.
4. Xác định khoảng đồng biến, nghịch biến:
Vì a = 1 > 0, parabol có dạng mở lên trên. Do đó:
5. Vẽ đồ thị hàm số:
Để vẽ đồ thị hàm số, ta cần xác định một số điểm thuộc đồ thị, chẳng hạn như:
Dựa vào các điểm đã xác định và tọa độ đỉnh, trục đối xứng, ta có thể vẽ được đồ thị hàm số.
Khi giải bài tập về hàm số bậc hai, học sinh cần chú ý các điểm sau:
Bài tập về hàm số bậc hai có nhiều ứng dụng trong thực tế, chẳng hạn như:
Hy vọng với lời giải chi tiết và phân tích kỹ lưỡng này, các em học sinh sẽ hiểu rõ hơn về Bài 2 trang 14 SGK Toán 11 tập 2 - Cánh Diều và tự tin giải các bài tập tương tự.