Bài 10 trang 21 SGK Toán 11 tập 1 - Cánh diều là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn của hàm số để giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 10 trang 21 SGK Toán 11 tập 1 - Cánh diều, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Có hai chung cư cao tầng xây cạnh nhau với khoảng cách giữa chúng là (HK = 20m). Để đảm bảo an ninh, trên nóc chung cư thứ hai người ta lắp camera ở vị trí C.
Đề bài
Có hai chung cư cao tầng xây cạnh nhau với khoảng cách giữa chúng là \(HK = 20m\). Để đảm bảo an ninh, trên nóc chung cư thứ hai người ta lắp camera ở vị trí C. Gọi A, B lần lượt là vị trí thấp nhất, cao nhất trên chung cư thứ nhất mà camera có thể quan sát được (Hình 19). Hãy tính số đo góc ACB (phạm vi camera có thể quan sát được ở chung cư thứ nhất). Biết rằng chiều cao của chung cư thứ hai là \(CK = 32m,AH = 6m,BH = 24m\) (làm tròn kết quả đến hàng phần mười theo đơn vị độ).
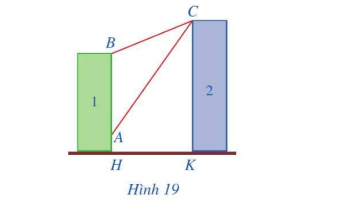
Phương pháp giải - Xem chi tiết
Dựa vào công thức cộng để tính
Lời giải chi tiết
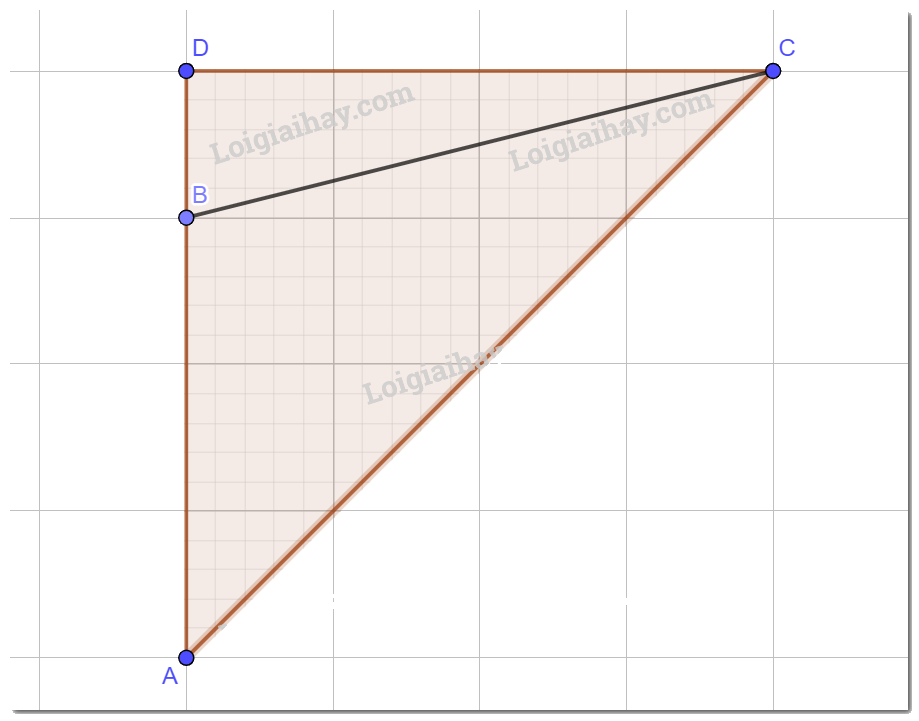
Từ C kẻ CD vuông góc với AB
Ta có: \(AD = CK - AH = 32 - 6 = 26\left( m \right)\)
\(\begin{array}{l}AB = BH - AH = 24 - 6 = 18\left( m \right)\\DB = AD - AB = 26 - 18 = 8\left( m \right)\end{array}\)
\(CD = HK = 20m\)
Ta có: \(\tan DCB = \frac{{DB}}{{CD}} = \frac{8}{{20}} = \frac{2}{5}\)
\(\tan DCA = \frac{{DA}}{{DC}} = \frac{{26}}{{20}} = \frac{{13}}{{10}}\)
\[\begin{array}{l}\tan BCA = \tan \left( {DCA - DCB} \right) = \frac{{\tan DCA - \tan DCB}}{{1 + \tan DCA.\tan DCB}} = \frac{{\frac{{13}}{{10}} - \frac{2}{5}}}{{1 + \frac{{13}}{{10}}.\frac{2}{5}}} = \frac{{45}}{{76}}\\ \Rightarrow \widehat {ACB} \approx 30,6^\circ \end{array}\]
Bài 10 trang 21 SGK Toán 11 tập 1 - Cánh diều thuộc chương trình học về giới hạn của hàm số. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản về giới hạn, các tính chất của giới hạn và các phương pháp tính giới hạn.
Bài tập yêu cầu tính giới hạn của hàm số tại một điểm cho trước. Các hàm số thường gặp trong bài tập này bao gồm hàm đa thức, hàm hữu tỉ và hàm lượng giác. Để tính giới hạn, học sinh có thể sử dụng các phương pháp sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi trong bài tập.
Lời giải:
Vậy, limx→2 (x2 - 4) / (x - 2) = 4
Lời giải:
Đây là một giới hạn lượng giác cơ bản. Sử dụng định lý giới hạn, ta có:
limx→0 sin(x) / x = 1
Kiến thức về giới hạn có ứng dụng rộng rãi trong nhiều lĩnh vực của Toán học, như giải tích, hình học và xác suất thống kê. Ngoài ra, giới hạn còn được sử dụng trong các lĩnh vực khác như vật lý, kinh tế và khoa học máy tính.
Bài 10 trang 21 SGK Toán 11 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn của hàm số. Hy vọng với lời giải chi tiết và phân tích chuyên sâu mà chúng tôi cung cấp, các bạn học sinh sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.