Bài 3 trang 115 SGK Toán 11 tập 2 thuộc chương trình Toán 11 Cánh Diều, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này đòi hỏi học sinh phải nắm vững các công thức đạo hàm cơ bản và kỹ năng giải toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ bản chất của bài toán và tự tin làm bài tập.
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình vuông cạnh \(a\). Góc giữa đường thẳng \(AC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \({60^ \circ }\).
Đề bài
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình vuông cạnh \(a\). Góc giữa đường thẳng \(AC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \({60^ \circ }\).
a) Chứng minh rằng hai mặt phẳng \(\left( {ACC'A'} \right)\) và \(\left( {BDD'B'} \right)\) vuông góc với nhau.
b) Tính khoảng cách giữa hai đường thẳng \(AB\) và \(CD'\).
Phương pháp giải - Xem chi tiết
‒ Cách chứng minh hai mặt phẳng vuông góc: Chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng còn lại.
‒ Cách tính khoảng cách giữa hai đường thẳng song song: Tính khoảng cách từ một điểm bất kì thuộc đường thẳng này đến đường thẳng kia.
Lời giải chi tiết
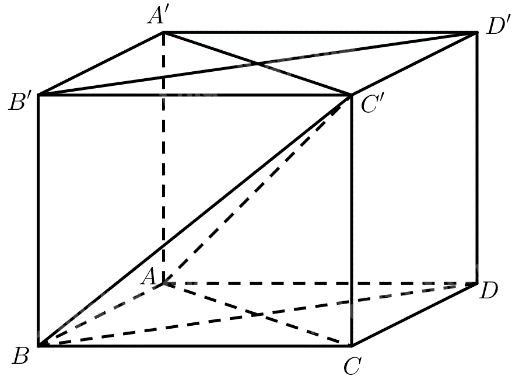
a) \(ABCD\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\(BB' \bot \left( {ABCD} \right) \Rightarrow BB' \bot AC\)
\(\left. \begin{array}{l} \Rightarrow AC \bot \left( {B{\rm{DD'B'}}} \right)\\AC \subset \left( {ACC'A'} \right)\end{array} \right\} \Rightarrow \left( {ACC'A'} \right) \bot \left( {B{\rm{DD}}'B'} \right)\)
b) \(ABCD\) là hình vuông \( \Rightarrow AB\parallel C{\rm{D}}\)
\(CDD'C'\) là hình chữ nhật \( \Rightarrow C{\rm{D}}\parallel C'{\rm{D}}'\)
\( \Rightarrow AB\parallel C'{\rm{D}}' \Rightarrow d\left( {AB,C'{\rm{D}}'} \right) = d\left( {B,C'{\rm{D}}'} \right)\)
\(A'B'C'D'\) là hình vuông \( \Rightarrow C'D' \bot B'C'\)
\(CDD'C'\) là hình chữ nhật \( \Rightarrow C'D' \bot CC'\)
\( \Rightarrow C'D' \bot \left( {BCC'B'} \right) \Rightarrow C'D' \bot BC' \Rightarrow d\left( {B,C'{\rm{D}}'} \right) = BC'\)
\(ABCD\) là hình vuông \( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
\(\begin{array}{l}CC' \bot \left( {ABCD} \right) \Rightarrow \left( {AC',\left( {ABCD} \right)} \right) = \left( {AC',AC} \right) = \widehat {CAC'} = {60^ \circ }\\ \Rightarrow CC' = AC.\tan \widehat {CAC'} = a\sqrt 6 \end{array}\)
\(\Delta BCC'\) vuông tại \(C \Rightarrow BC{'^2} = \sqrt {B{C^2} + CC{'^2}} = a\sqrt 7 \)
Vậy \(d\left( {AB,C'{\rm{D}}'} \right) = a\sqrt 7 \).
Bài 3 trang 115 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến tốc độ thay đổi của hàm số. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
(Đề bài Bài 3 trang 115 SGK Toán 11 tập 2 - Cánh Diều được trình bày đầy đủ tại đây)
Để giải bài tập này, chúng ta cần thực hiện các bước sau:
(Lời giải chi tiết cho từng ý của bài tập được trình bày tại đây, bao gồm các bước tính toán, giải thích rõ ràng và sử dụng các ký hiệu toán học chính xác.)
Để giải nhanh bài tập này, bạn có thể sử dụng một số mẹo sau:
Để hiểu rõ hơn về cách giải bài tập này, chúng ta hãy xem xét một ví dụ minh họa:
(Ví dụ minh họa được trình bày tại đây, bao gồm đề bài, lời giải chi tiết và giải thích rõ ràng.)
Để rèn luyện kỹ năng giải bài tập về đạo hàm, bạn có thể làm thêm một số bài tập tương tự sau:
Bài 3 trang 115 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và rèn luyện kỹ năng giải toán. Hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập này, các bạn học sinh sẽ tự tin hơn trong việc học tập môn Toán.
Lưu ý:
Chúc các bạn học tốt!