Lý thuyết Khoảng cách - Toán 11 Cánh diều

Chào mừng bạn đến với bài học về Lý thuyết Khoảng cách trong chương trình Toán 11 Cánh diều. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về các khái niệm khoảng cách trong không gian, bao gồm khoảng cách từ một điểm đến một đường thẳng và khoảng cách giữa hai đường thẳng.

Chúng tôi sẽ trình bày lý thuyết một cách dễ hiểu, kèm theo các ví dụ minh họa cụ thể để giúp bạn nắm bắt kiến thức một cách nhanh chóng và hiệu quả. Đây là nền tảng quan trọng để giải quyết các bài toán hình học không gian phức tạp hơn.

1. Khoảng cách từ một điểm đến một đường thẳng Cho đường thẳng \(\Delta \) và điểm \(M\) không thuộc \(\Delta \).

1. Khoảng cách từ một điểm đến một đường thẳng

Cho đường thẳng \(\Delta \) và điểm \(M\) không thuộc \(\Delta \). Gọi \(H\) là hình chiếu của điểm \(M\) trên đường thẳng \(\Delta \). Độ dài đoạn thẳng MH gọi là khoảng cách từ điểm \(M\) đến đường thẳng \(\Delta \), kí hiệu \(d(M,\Delta )\).

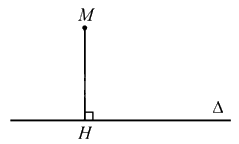
Lý thuyết Khoảng cách - Toán 11 Cánh diều 1

Chú ý: Khi điểm \(M\) thuộc đường thẳng \(\Delta \) thì \(d(M,\Delta ) = 0.\)

2. Khoảng cách từ một điểm đến một mặt phẳng

Cho mặt phẳng \((P)\) và điểm \(M\) không thuộc mặt phẳng \((P)\). Gọi \(H\) là hình chiếu của \(M\) trên mặt phẳng \((P)\). Độ dài đoạn thẳng MH gọi là khoảng cách từ điểm \(M\) đến mặt phẳng \((P)\), kí hiệu \(d(M,(P))\).

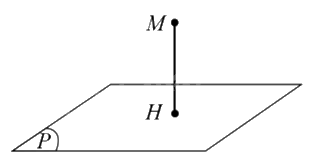
Lý thuyết Khoảng cách - Toán 11 Cánh diều 2

Chú ý: Khi điểm \(M\) thuộc mặt phẳng \((P)\) thì \(d(M,(P)) = 0.\)

3. Khoảng cách giữa hai đường thẳng song song

Khoảng cách giữa hai đường thẳng song song \(\Delta ,\Delta '\) là khoảng cách từ một điểm bất kì thuộc đường thẳng này đến đường thẳng kia, kí hiệu \(d\left( {\Delta ,{\Delta ^\prime }} \right)\).

Ví dụ: Trong hình dưới đây, ta có: \(d\left( {\Delta ,{\Delta ^\prime }} \right) = AB\) với \(A \in \Delta \), \(B \in {\Delta ^\prime },AB \bot \Delta ,AB \bot {\Delta ^\prime }\) và \(\Delta //{\Delta ^\prime }\).

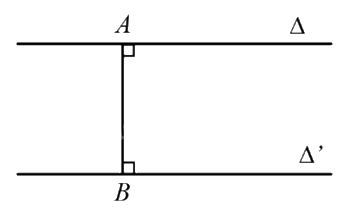
Lý thuyết Khoảng cách - Toán 11 Cánh diều 3

4. Khoảng cách giữa đường thẳng và mặt phẳng song song

Cho đường thẳng \(\Delta \) song song với mặt phẳng \((P)\). Khoảng cách giữa đường thẳng \(\Delta \) và mặt phẳng \((P)\) là khoảng cách từ một điểm bất kì thuộc đường thẳng \(\Delta \) đến mặt phẳng \((P)\), kí hiệu \(d(\Delta ,(P))\).

Ví dụ: Trong hình dưới đây, ta có: \(d(\Delta ,(P)) = M{M^\prime } = h\), trong đó \(M \in \Delta ,{M^\prime } \in (P),M{M^\prime } \bot (P)\) và \(\Delta //(P)\).

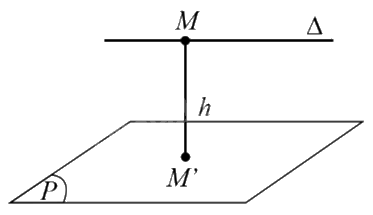
Lý thuyết Khoảng cách - Toán 11 Cánh diều 4

5. Khoảng cách giữa hai mặt phẳng song song

Khoảng cách giữa hai mặt phẳng song song \((P),(Q)\) là khoảng cách từ một điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia, kí hiệu \(d((P),(Q))\).

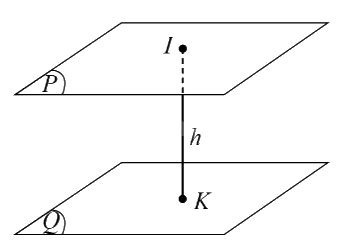
Ví dụ: Trong hình dưới đây, ta có: \(d((P),(Q)) = IK = h\) với \(I \in (P),K \in (Q),IK \bot (P),IK \bot (Q)\) và \((P)//(Q)\).

Lý thuyết Khoảng cách - Toán 11 Cánh diều 5

6. Khoảng cách giữa hai đưò̀ng thẳng chéo nhau

Cho hai đường thẳng a, b chéo nhau.

- Đường thẳng c vừa vuông góc, vừa cắt cả hai đường thẳng a và b được gọi là đường vuông góc chung của hai đường thẳng đó.

- Đoạn thẳng có hai đầu mút là giao điểm của đường thẳng c với hai đường thẳng a, b được gọi là đoạn vuông góc chung của hai đường thẳng đó.

- Độ dài đoạn thẳng vuông góc chung của hai đường thẳng a, b gọi là khoảng cách giữa hai đường thẳng đó, kí hiệu \(d(a,b)\).

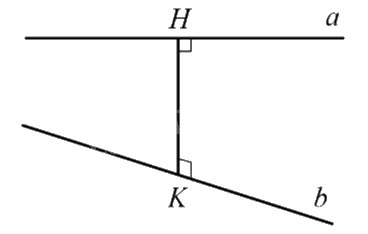
Ví dụ: Trong hình dưới đây, ta có: \(d(a,b) = HK\) với HK là đoạn vuông góc chung của \(a\) và \(b\).

Lý thuyết Khoảng cách - Toán 11 Cánh diều 6

Lý thuyết Khoảng cách - Toán 11 Cánh diều 7

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Lý thuyết Khoảng cách - Toán 11 Cánh diều – hành trang không thể thiếu trong chuyên mục Ôn tập Toán lớp 11 trên nền tảng toán. Bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Lý thuyết Khoảng cách - Toán 11 Cánh diều

Trong chương trình Toán 11 Cánh diều, phần Lý thuyết Khoảng cách đóng vai trò quan trọng trong việc xây dựng nền tảng kiến thức về hình học không gian. Nắm vững lý thuyết này sẽ giúp học sinh giải quyết các bài toán liên quan đến vị trí tương đối của điểm, đường thẳng và mặt phẳng một cách hiệu quả.

1. Khoảng cách từ một điểm đến một đường thẳng

Khoảng cách từ điểm M(x₀, y₀) đến đường thẳng Δ: ax + by + c = 0 được tính theo công thức:

d(M, Δ) = |ax₀ + by₀ + c| / √(a² + b²)

Công thức này dựa trên việc tìm hình chiếu vuông góc của điểm M lên đường thẳng Δ và tính độ dài đoạn thẳng nối M với hình chiếu đó.

2. Khoảng cách giữa hai đường thẳng song song

Nếu hai đường thẳng Δ₁: ax + by + c₁ = 0 và Δ₂: ax + by + c₂ = 0 song song với nhau, khoảng cách giữa chúng được tính theo công thức:

d(Δ₁, Δ₂) = |c₂ - c₁| / √(a² + b²)

Lưu ý rằng hai đường thẳng phải có cùng hệ số a và b để được coi là song song.

3. Khoảng cách giữa hai đường thẳng chéo nhau

Đây là phần phức tạp hơn, đòi hỏi việc tìm đường vuông góc chung của hai đường thẳng. Có nhiều phương pháp để tìm đường vuông góc chung, bao gồm:

Phương pháp vector: Sử dụng tích vô hướng và tích có hướng để tìm vector chỉ phương của đường vuông góc chung.
Phương pháp hình học: Xây dựng các mặt phẳng chứa một đường thẳng và vuông góc với đường thẳng còn lại.

Sau khi tìm được đường vuông góc chung, khoảng cách giữa hai đường thẳng chính là độ dài đoạn thẳng nối hai điểm thuộc hai đường thẳng và nằm trên đường vuông góc chung.