Bài 2 trang 77 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Cánh Diều, tập trung vào việc rèn luyện kỹ năng giải bài tập về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để tính đạo hàm của hàm số, đồng thời hiểu rõ ý nghĩa hình học của đạo hàm.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
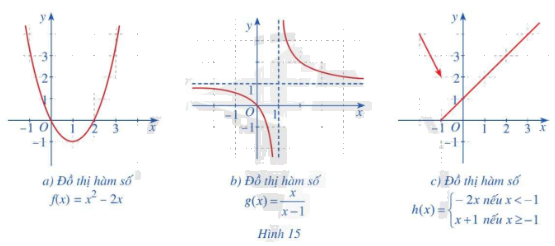
Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c, hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích.
Đề bài
Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c, hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích.
Phương pháp giải - Xem chi tiết
- Các hàm đa thức liên tục trên \(\mathbb{R}\)
- Các hàm phân thức hữu tỉ liên tục trên từng khoảng xác định của chúng
- Hàm số \(y = f\left( x \right)\) được gọi là liên tục tại \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Lời giải chi tiết
+) Hình 15a: Hàm số \(f\left( x \right) = {x^2}\;-2x\) có tập xác định \(D = \mathbb{R}.\)
Hàm số liên tục trên \(\mathbb{R}.\)
+) Hình 15b: Hàm số \(g\left( x \right) = \frac{x}{{x - 1}}\) có tập xác định \(D = \mathbb{R}\backslash \left\{ 1 \right\}.\)
Vậy hàm số liên tục trên các khoảng \(\left( {-\infty ;1} \right)\)và \(\left( {1; + \infty } \right).\)
+) Hình 15c:
Với \(x\; \in \;\left( {-\infty ;-1} \right)\) có \(f\left( x \right) = -2x\) liên tục với mọi \(x\; \in \;\left( {-\infty ;-1} \right)\)
Với \(x\; \in \;\left( {-1; + \infty } \right)\) có \(f\left( x \right) = x + 1\) liên tục với mọi \(x\; \in \;\left( {-1; + \infty } \right)\)
Tại x = – 1 có
\(\begin{array}{l}\mathop {\lim }\limits_{x \to - 1} f\left( x \right) = \mathop {\lim }\limits_{x \to - 1} \left( {2x} \right) = 2.\left( { - 1} \right) = - 2\\f\left( { - 1} \right) = - 1 + 1 = 0\\ \Rightarrow \mathop {\lim }\limits_{x \to - 1} f\left( x \right) \ne f\left( { - 1} \right)\end{array}\)
Do đó hàm số không liên tục tại x = – 1.
Vậy hàm số liên tục trên các khoảng \(\left( {-\infty ;-1} \right)\)và \(\left( {-1; + \infty } \right).\)
Bài 2 trang 77 SGK Toán 11 tập 1 - Cánh Diều yêu cầu học sinh tính đạo hàm của các hàm số đã cho. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc tính đạo hàm cơ bản, bao gồm đạo hàm của tổng, hiệu, tích, thương và đạo hàm của hàm hợp.
Bài tập bao gồm các hàm số với nhiều dạng khác nhau, từ hàm số đơn giản đến hàm số phức tạp. Việc phân tích đúng dạng hàm số là bước quan trọng để lựa chọn phương pháp tính đạo hàm phù hợp.
Để giải bài tập này, chúng ta sẽ sử dụng các quy tắc tính đạo hàm sau:
Câu a: y = x3 - 3x2 + 2x - 5
Áp dụng quy tắc đạo hàm của tổng/hiệu, ta có:
y' = (x3)' - 3(x2)' + 2(x)' - (5)'
y' = 3x2 - 6x + 2 - 0
y' = 3x2 - 6x + 2
Câu b: y = (x2 + 1)(x - 2)
Áp dụng quy tắc đạo hàm của tích, ta có:
y' = (x2 + 1)'(x - 2) + (x2 + 1)(x - 2)'
y' = 2x(x - 2) + (x2 + 1)(1)
y' = 2x2 - 4x + x2 + 1
y' = 3x2 - 4x + 1
Câu c: y = x / (x + 1)
Áp dụng quy tắc đạo hàm của thương, ta có:
y' = ((x)'(x + 1) - x(x + 1)') / (x + 1)2
y' = (1(x + 1) - x(1)) / (x + 1)2
y' = (x + 1 - x) / (x + 1)2
y' = 1 / (x + 1)2
Khi tính đạo hàm, cần chú ý đến các quy tắc ưu tiên. Ví dụ, khi gặp biểu thức có phép nhân và phép cộng, ta cần thực hiện phép nhân trước, sau đó mới thực hiện phép cộng.
Để củng cố kiến thức, học sinh có thể tự giải các bài tập tương tự trong SGK và sách bài tập Toán 11 tập 1 - Cánh Diều. Ngoài ra, học sinh cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán uy tín.
Đạo hàm có nhiều ứng dụng quan trọng trong toán học và các lĩnh vực khác, bao gồm:
Bài 2 trang 77 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm. Bằng cách nắm vững các quy tắc tính đạo hàm và áp dụng chúng một cách linh hoạt, học sinh có thể giải quyết bài tập này một cách hiệu quả và tự tin hơn trong quá trình học tập.