Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho Bài 5 trang 120 SGK Toán 11 tập 1 - Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin đối mặt với các bài tập trong chương trình học.
Chúng tôi cam kết mang đến cho bạn trải nghiệm học toán online tốt nhất với đội ngũ giáo viên giàu kinh nghiệm và phương pháp giảng dạy tiên tiến.
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, BD. Điểm P thuộc cạnh AC sao cho PA = 2PC
Đề bài
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, BD. Điểm P thuộc cạnh AC sao cho PA = 2PC
a) Xác định giao điểm E của đường thẳng MP với mặt phẳng (BCD)
b) Xác định giao điểm Q của đường thẳng CD với mặt phẳng (MNP)
c) Xác định giao tuyến của mặt phẳng (ACD) với mặt phẳng (MNP).
d) Gọi I là giao điểm của MQ và NP, G là trọng tâm của tam giác ABD. Chứng minh rằng C, I, G thẳng hàng.
Phương pháp giải - Xem chi tiết
a,b, Tìm giao điểm của đường thẳng a và mặt phẳng (P) ta làm như sau: + Tìm mặt phẳng (Q) chứa a.
+ Tìm giao tuyến d của (P) và (Q).
+ Giao tuyến d cắt đường thẳng a tại I.
Suy ra, I là giao điểm của đường thẳng a và mặt phẳng (P).
c, Tìm 2 điểm cùng thuộc 2 mặt phẳng đó. Đường thẳng đi qua 2 điểm đó chính là giao tuyến của 1 mặt phẳng.
d, Chứng minh 3 điểm cùng thuộc 1 đường thẳng.
Lời giải chi tiết
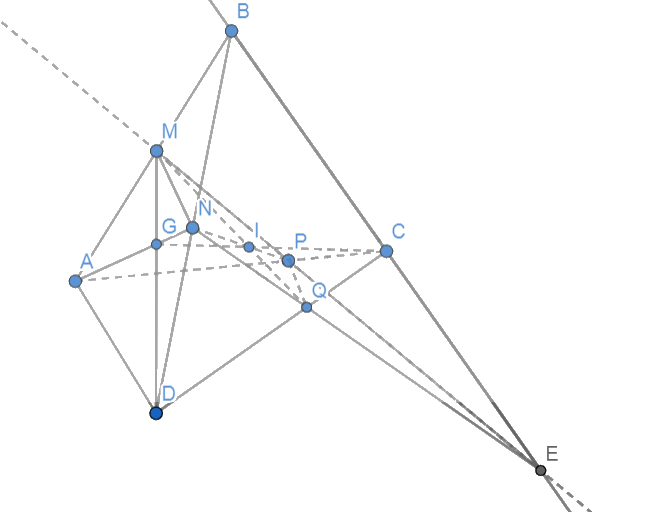
a) Trong mp(ABC), kéo dài MP cắt BC tại E. Nối AE, DE.
Ta có: MP ∩ BC = {E};
BC ⊂ (BCD)
Do đó MP ∩ (BCD) = {E}.
b) Nối NE, NE cắt CD tại Q.
Ta có: CD ∩ NE = {Q};
NE ⊂ (MNP)
Do đó CD ∩ (MNP) = {Q}.
c) Ta có: P ∈ AC, mà AC ⊂ (ACD) nên P ∈ (ACD);
Mà P ∈ (MNP) nên P là giao điểm của (ACD) và (MNP).
Lại có Q ∈ CD và CD ⊂ (ACD) nên Q ∈ (ACD);
Mà Q ∈ (MNP) nên Q là giao điểm của (ACD) và (MNP).
Do đó PQ là giao tuyến của hai mặt phẳng (ACD) và (MNP).
d) Do G là trọng tâm của tam giác ABD nên hai đường trung tuyến DM, AN của tam giác cùng đi qua G.
Ta có: G ∈ AN mà AN ⊂ (ANC) nên G ∈ (ANC);
G ∈ DM mà DM ⊂ (MDC) nên G ∈ (MDC).
Do đó G là giao điểm của hai mặt phẳng (ANC) và (MDC).
Lại có: C ∈ (ANC) và C ∈ (MDC) nên C cũng là giao điểm của hai mặt phẳng (ANC) và (MDC).
Vậy GC là giao tuyến của hai mặt phẳng (ANC) và (MDC).
Mặt khác, I là giao điểm của MQ và NP nên I ∈ MQ và I ∈ NP.
Vì I ∈ MQ mà MQ ⊂ (MDC) nên I ∈ (MDC)
Vì I ∈ NP mà NP ⊂ (ANC) nên I ∈ (ANC)
Do đó giao tuyến GC của hai mặt phẳng (ANC) và (MDC) đi qua điểm I.
Vậy ba điểm C, I, G thẳng hàng.
Bài 5 trang 120 SGK Toán 11 tập 1 - Cánh Diều thuộc chương trình học về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về định nghĩa giới hạn, các tính chất của giới hạn để tính toán và chứng minh các biểu thức liên quan đến giới hạn.
Để giải quyết bài tập này một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
Ví dụ 1: Tính limx→2 (x2 - 4) / (x - 2)
Giải:
limx→2 (x2 - 4) / (x - 2) = limx→2 (x - 2)(x + 2) / (x - 2) = limx→2 (x + 2) = 2 + 2 = 4
Ví dụ 2: Chứng minh limx→0 sin(x) / x = 1
Giải:
Chứng minh này sử dụng định lý kẹp (squeeze theorem) và kiến thức về hình học lượng giác. (Giải thích chi tiết chứng minh bằng định lý kẹp)
Để củng cố kiến thức và kỹ năng giải toán, bạn nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập khác với lời giải chi tiết, giúp bạn tự tin hơn trong quá trình học tập.
Bài 5 trang 120 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng giúp học sinh hiểu sâu hơn về giới hạn của hàm số. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên, bạn đã có thể tự tin giải quyết bài tập này một cách hiệu quả. Chúc bạn học tốt!