Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau đi sâu vào giải chi tiết các bài tập trong mục 4, trang 102 và 103 sách giáo khoa Toán 11 tập 2 - Cánh Diều.
Mục tiêu của chúng tôi là cung cấp cho các em những lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Trong Hình 67, thanh gỗ dọc phía trên các cột và mặt đường hành lang gợi nên hình ảnh đường thẳng \(\Delta \) và mặt phẳng \(\left( P \right)\)
Trong Hình 67, thanh gỗ dọc phía trên các cột và mặt đường hành lang gợi nên hình ảnh đường thẳng \(\Delta \) và mặt phẳng \(\left( P \right)\) song song với nhau, chiều cao của chiếc cột có đỉnh cột \(A\) là khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( P \right)\).
a) Khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( P \right)\) có phụ thuộc vào vị trí của điểm \(A\) trên đường thẳng \(\Delta \) hay không? Vì sao?
b) Khoảng cách đó gợi nên khái niệm nào trong hình học liên quan đến đường thẳng \(\Delta \) và mặt phẳng \(\left( P \right)\)?
Phương pháp giải:
Sử dụng tính chất của đường thẳng và mặt phẳng song song.
Lời giải chi tiết:
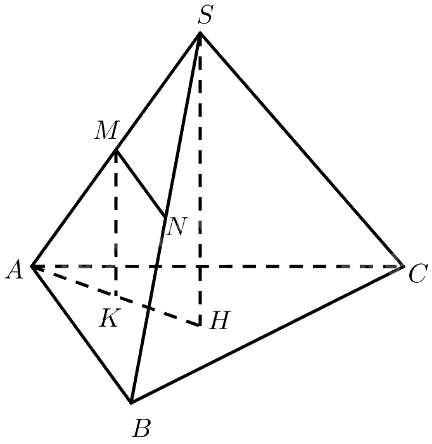
a) Trên đường thẳng \(\Delta \) lấy điểm \(B\) khác \(A\).
Kẻ \(AH \bot \left( P \right),BK \bot \left( P \right)\left( {H,K \in \left( P \right)} \right)\)
\( \Rightarrow ABKH\) là hình chữ nhật \( \Rightarrow AH = BK\)
\( \Rightarrow d\left( {A,\left( P \right)} \right) = d\left( {B,\left( P \right)} \right)\)
Vậy khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( P \right)\) không phụ thuộc vào vị trí của điểm \(A\) trên đường thẳng \(\Delta \).
b) Khoảng cách đó gợi nên khái niệm khoảng cách giữa đường thẳng và mặt phẳng song song.
Cho hình chóp \(S.ABC\) có \(SA = a\), góc giữa \(SA\) và \(mp\left( {ABC} \right)\) là \({60^ \circ }\). Gọi \(M,N\) lần lượt là trung điểm của cạnh \(SA\) và \(SB\). Chứng minh \(MN\parallel \left( {ABC} \right)\) và tính \(d\left( {MN,\left( {ABC} \right)} \right)\).
Phương pháp giải:
‒ Cách chứng minh đường thẳng song song với mặt phẳng: Chứng minh đường thẳng đó song song với một đường thẳng nằm trên mặt phẳng.
‒ Cách tính khoảng cách giữa đường thẳng và mặt phẳng song song: Tính khoảng cách từ một điểm trên đường thẳng đến mặt phẳng.
Lời giải chi tiết:

Ta có: \(M\) là trung điểm của \(SA\)
\(N\) là trung điểm của \(SB\)
\( \Rightarrow MN\) là đường trung bình của \(\Delta SAB\)
\(\left. \begin{array}{l} \Rightarrow MN\parallel AB\\AB \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {ABC} \right)\)
\( \Rightarrow d\left( {MN,\left( {ABC} \right)} \right) = d\left( {M,\left( {ABC} \right)} \right)\)
Gọi \(H\) là hình chiếu vuông góc của \(S\) lên \(\left( {ABC} \right)\)\( \Rightarrow SH \bot \left( {ABC} \right)\)
Qua \(M\) kẻ đường thẳng song song với \(SH\), cắt \(\left( {ABC} \right)\) tại \(K\)
\( \Rightarrow K \in AH,MK \bot \left( {ABC} \right) \Rightarrow d\left( {M,\left( {ABC} \right)} \right) = MK\)
\(\begin{array}{l}SH \bot \left( {ABC} \right) \Rightarrow \left( {SA,\left( {ABC} \right)} \right) = \left( {SA,HA} \right) = \widehat {SAH} = {60^ \circ }\\ \Rightarrow SH = SA.\sin \widehat {SAH} = \frac{{a\sqrt 3 }}{2}\end{array}\)
\(M\) là trung điểm của \(SA\), \(MK\parallel SH\)
\( \Rightarrow MK\) là đường trung bình của \(\Delta SAH\)
\( \Rightarrow MK = \frac{1}{2}AH = \frac{{a\sqrt 3 }}{4}\)
Vậy \(d\left( {MN,\left( {ABC} \right)} \right) = \frac{{a\sqrt 3 }}{4}\)
Mục 4 của chương trình Toán 11 tập 2 - Cánh Diều tập trung vào các kiến thức về phép biến hình. Cụ thể, các em sẽ được làm quen với các phép biến hình cơ bản như phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các kiến thức này là vô cùng quan trọng, không chỉ để giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng cho các kiến thức nâng cao hơn trong chương trình học.
Bài tập 1 yêu cầu các em vận dụng kiến thức về phép tịnh tiến để tìm ảnh của một điểm, một đường thẳng hoặc một hình. Để giải quyết bài tập này, các em cần nắm vững công thức của phép tịnh tiến: x' = x + a, y' = y + b, trong đó (a, b) là vectơ tịnh tiến.
Ví dụ, cho điểm A(1, 2) và vectơ tịnh tiến v = (3, -1). Tìm tọa độ điểm A' là ảnh của A qua phép tịnh tiến theo vectơ v. Giải: x' = 1 + 3 = 4, y' = 2 - 1 = 1. Vậy A'(4, 1).
Bài tập 2 tập trung vào việc ứng dụng phép quay để giải quyết các bài toán hình học. Các em cần hiểu rõ công thức của phép quay quanh gốc tọa độ O(0, 0) với góc quay α: x' = xcosα - ysinα, y' = xsinα + ycosα.
Để giải bài tập này, các em cần chú ý đến việc xác định đúng tâm quay, góc quay và tọa độ của điểm cần tìm ảnh.
Bài tập 3 yêu cầu các em tìm hiểu về phép đối xứng trục và ứng dụng vào giải các bài toán thực tế. Công thức của phép đối xứng trục d: ax + by + c = 0 là: x' = x - 2a(ax + by + c) / (a2 + b2), y' = y - 2b(ax + by + c) / (a2 + b2).
Các em cần nắm vững cách xác định phương trình đường thẳng đối xứng và áp dụng công thức một cách chính xác.
Bài tập 4 liên quan đến phép đối xứng tâm I(x0, y0). Công thức của phép đối xứng tâm I là: x' = 2x0 - x, y' = 2y0 - y.
Để giải bài tập này, các em cần xác định đúng tâm đối xứng và áp dụng công thức một cách chính xác.
Phép biến hình không chỉ là một phần quan trọng trong chương trình Toán học mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau như:
Hy vọng rằng với những giải thích chi tiết và hướng dẫn cụ thể trên đây, các em đã có thể tự tin giải quyết các bài tập trong mục 4 trang 102, 103 SGK Toán 11 tập 2 - Cánh Diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!