Chào mừng các em học sinh đến với lời giải Bài 1 trang 113 SGK Toán 11 tập 1 - Cánh Diều. Bài học này thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến kiến thức đã học.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự. Hãy cùng chúng tôi khám phá lời giải ngay sau đây!
Cho hình hộp ABCD.A’B’C’D’.
Đề bài
Cho hình hộp ABCD.A’B’C’D’.
a) Chứng minh rằng (ACB’) // (A’C’D’)
b) Gọi\({G_1},{G_2}\)lần lượt là giao điểm của BD’ với các mặt phẳng (ACB’) và (A’C’D’).
Chứng minh rằng\({G_1},{G_2}\)lần lượt là trọng tâm của hai tam giác ACB’ và A’C’D.
c) Chứng minh rằng \(B{G_1} = {G_1}{G_2} = D'{G_2}\)
Phương pháp giải - Xem chi tiết
Nếu mặt phẳng (P) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q)
Lời giải chi tiết
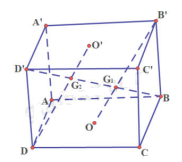
a) Ta có: AD // B’C’, AD = B’C’ nên ADC’B’ là hình bình hành
Suy ra AB’ // DC’ nên AB‘ // (A’C’D) (1)
Ta có: (ACC’A‘) là hình bình hành nên AC // A’C‘
Suy ra AC // (A’C’D‘) (2)
Mà AB‘, AC thuộc (ACB‘) (3)
Từ (1), (2), (3) suy ra (ACB‘) // (A‘C’D)
b) Gọi O, O’ lần lượt là tâm hình bình hành ABCD, A’B’C’D’
Trong (BDD’B’): B’O cắt BD’
Mà B’O thuộc (ACB’), BD’ cắt (ACB’) tại\({G_1}\)
Suy ra: B’O cắt BD’ tại\({G_1}\)
Tương tự, ta có: DO’ cắt BD’ tại\({G_2}\)
Ta có: tam giác \({G_1}OB\) đồng dạng với tam giác \({G_1}B'D'\) (do BD // B’D’)
Suy ra\(\frac{{{G_1}O}}{{{G_1}B'}} = \frac{{OB}}{{B'D'}} = \frac{1}{2}\)
Nên \(\frac{{{G_1}O}}{{{G_1}B'}} = \frac{2}{3}\)
Do đó:\({G_1}\) là trọng tâm tam giác ACB’
Chứng minh tương tự ta có:\({G_2}\) là trọng tâm tam giác A’C’D
c) Ta có tam giác\({G_1}OB\) đồng dạng với tam giác \({G_1}B'D'\)
Suy ra\(\frac{{{G_1}O}}{{{G_1}B'}} = \frac{{OB}}{{B'D'}} = \frac{1}{2}\)
Nên \({G_1}B = \frac{1}{3}BD'(1)\)
Tương tự ta có:\(\frac{{{G_2}D'}}{{{G_2}B}} = \frac{{OD'}}{{DB}} = \frac{1}{2}\)
Nên \({G_2}D' = \frac{1}{3}{\rm{DD}}'(2)\)
Từ (1) và (2) suy ra\({G_1}B = {G_1}{G_2} = {G_2}D'\)
Bài 1 trang 113 SGK Toán 11 tập 1 - Cánh Diều yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Bài tập này không chỉ giúp củng cố lý thuyết mà còn rèn luyện kỹ năng tính toán và tư duy logic.
Bài 1 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh:
Để giải bài tập này, chúng ta cần nắm vững các công thức và quy tắc đạo hàm cơ bản. Dưới đây là lời giải chi tiết cho từng câu hỏi:
Áp dụng quy tắc đạo hàm của tổng và hiệu, ta có:
f'(x) = 3x2 - 4x + 5
Hàm số g(x) xác định khi và chỉ khi biểu thức dưới dấu căn lớn hơn hoặc bằng 0:
x - 2 ≥ 0 ⇔ x ≥ 2
Vậy tập xác định của hàm số g(x) là [2, +∞).
Hàm số h(x) không xác định khi mẫu số bằng 0:
x + 1 = 0 ⇔ x = -1
Vậy hàm số h(x) có một điểm không xác định tại x = -1.
Để hiểu sâu hơn về đạo hàm, các em có thể tham khảo thêm các tài liệu sau:
Khi giải các bài tập về đạo hàm, các em cần lưu ý những điều sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Để rèn luyện thêm kỹ năng giải bài tập về đạo hàm, các em có thể thử giải các bài tập sau:
Hy vọng với lời giải chi tiết này, các em sẽ hiểu rõ hơn về Bài 1 trang 113 SGK Toán 11 tập 1 - Cánh Diều và tự tin giải các bài tập tương tự. Chúc các em học tập tốt!
| Công thức | Mô tả |
|---|---|
| (xn)' = nxn-1 | Đạo hàm của lũy thừa |
| (u + v)' = u' + v' | Đạo hàm của tổng |
| (u - v)' = u' - v' | Đạo hàm của hiệu |