Bài 5 trang 40 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 tập 1, Cánh diều. Bài tập này tập trung vào việc rèn luyện kỹ năng về giới hạn của hàm số, một khái niệm quan trọng trong giải tích.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và phương pháp giải bài tập này một cách hiệu quả.
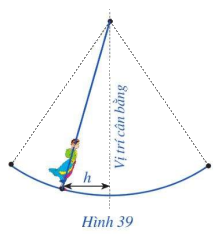
Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu.
Đề bài
Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động quanh vị trí cân bằng (Hình 39). Nghiên cứu trò chơi này, người ta thấy khoảng cách h (m) từ vị trí người chơi đu đến vị trí cân bằng được biểu diễn qua thời gian t (s) (với \(t \ge 0\)) bởi hệ thức \(h = \left| d \right|\) với \(d = 3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right]\), trong đó ta quy ước d > 0 khi vị trí cân bằng ở phía sau lưng người chơi đu và d < 0 trong trường hợp ngược lại. Vào thời gian t nào thì khoảng cách h là 3m; 0m?
Phương pháp giải - Xem chi tiết
Sử dụng công thức tổng quát để giải phương trình hàm số cos.
Lời giải chi tiết
+) Khi khoảng cách từ người chơi đu đến vị trí cân bằng là 3m thì h = 3.
Khi đó
\(\begin{array}{l}3 = \left| d \right| = \left| {3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right]} \right|\\ \Rightarrow \left[ \begin{array}{l}3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 3\\3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = - 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 1\\\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = - 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = \cos 0\\\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = \cos \pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{3}\left( {2t - 1} \right) = k2\pi \\\frac{\pi }{3}\left( {2t - 1} \right) = \pi + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}t = \frac{{6k + 1}}{2}\\t = 3k + 2\end{array} \right.;k \in Z\end{array}\)
+) Khi khoảng cách từ người chơi đu đến vị trí cân bằng là 0m thì h = 0.
Khi đó
\(\begin{array}{l}0 = \left| d \right| = \left| {3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right]} \right|\\ \Rightarrow 3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 0\\ \Leftrightarrow \cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 0\\ \Leftrightarrow \cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 0\\ \Leftrightarrow \cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = \cos \frac{\pi }{2}\\ \Leftrightarrow \frac{\pi }{3}\left( {2t - 1} \right) = \frac{\pi }{2} + k\pi \\ \Leftrightarrow t = \frac{5}{4} + \frac{{3k}}{2};k \in Z\end{array}\)
Bài 5 trang 40 SGK Toán 11 tập 1 - Cánh diều yêu cầu học sinh tính giới hạn của hàm số tại một điểm. Để giải bài tập này, học sinh cần nắm vững các định nghĩa và tính chất của giới hạn hàm số, cũng như các phương pháp tính giới hạn thường gặp.
Bài tập thường bao gồm các dạng sau:
Để giải bài 5 trang 40, ta cần xác định đúng dạng của hàm số và lựa chọn phương pháp phù hợp. Ví dụ, nếu hàm số là phân thức, ta có thể thử rút gọn phân thức trước khi tính giới hạn. Nếu hàm số chứa căn thức, ta có thể nhân liên hợp để khử căn thức.
Ví dụ minh họa:
Giả sử bài tập yêu cầu tính limx→2 (x2 - 4) / (x - 2)
Vậy, limx→2 (x2 - 4) / (x - 2) = 4
Khi tính giới hạn, cần chú ý đến các trường hợp sau:
Để củng cố kiến thức, học sinh có thể làm thêm các bài tập tương tự trong SGK và sách bài tập Toán 11 tập 1 - Cánh diều. Ngoài ra, học sinh cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán uy tín.
Giới hạn hàm số là một khái niệm cơ bản trong giải tích, có nhiều ứng dụng trong các lĩnh vực khác nhau như vật lý, kinh tế, và kỹ thuật. Ví dụ, giới hạn hàm số được sử dụng để tính đạo hàm, tích phân, và để mô tả các hiện tượng vật lý như vận tốc, gia tốc, và dòng điện.
Bài 5 trang 40 SGK Toán 11 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính giới hạn hàm số. Bằng cách nắm vững các định nghĩa, tính chất, và phương pháp tính giới hạn, học sinh có thể giải quyết bài tập này một cách hiệu quả và áp dụng kiến thức vào các bài toán thực tế.