Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 2 trang 106, 107, 108 sách giáo khoa Toán 11 tập 1 - Cánh Diều.
Mục tiêu của chúng tôi là cung cấp cho các em những lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho hai mặt phẳng phân biệt (P) và (Q). Mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và a, b cùng song song với mặt phẳng (Q) (Hình 61). Hai mặt phẳng (P) và (Q) có điểm chung hay không?
Cho hai mặt phẳng phân biệt (P) và (Q). Mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và a, b cùng song song với mặt phẳng (Q) (Hình 61). Hai mặt phẳng (P) và (Q) có điểm chung hay không?
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
Hai mặt phẳng (P) và (Q) không có điểm chung
Cho tứ diện ABCD. Các điểm M, N, P, I, J, K lần lượt là trung điểm của BC, CD, DB, AM, AN, AP. Chứng minh rằng (IJK) // (BCD).
Phương pháp giải:
Nếu mặt phẳng (P) chứa hai đường thẳng cắt nhau a, b và a,b cùng song song với mặt phẳng (Q) thì (P) song song với (Q)
Lời giải chi tiết:

Tam giác AMP có: I, K là trung điểm AM, AP
Suy ra: IK // MP
Suy ra IK // (BCD) (1)
Tam giác ANP có: J, K là trung điểm AN, AP
Suy ra: JK // NP
Suy ra: JK // (BCD) (2)
Từ (1) và (2) suy ra: (IJK) // (BCD)
Cho mặt phẳng (Q) và điểm M nằm ngoài mặt phẳng (Q).
a) Trong mặt phẳng (Q) vẽ hai đường thẳng a’, b’ cắt nhau. Qua điểm M kẻ các đường thẳng a, và b lần lượt song song với a’, b’. Gọi (P) là mặt phẳng xác định bởi hai đường thẳng (cắt nhau) a và b (Hình 63). Mặt phẳng (P) có song song với mặt phẳng (Q) hay không?
b) Xét mặt phẳng (R) đi qua điểm M và song song với mặt phẳng (Q). Hai mặt phẳng (R) và (P) có trùng nhau hay không?

Phương pháp giải:
Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.
Lời giải chi tiết:
a) Mặt phẳng (P) song song với mặt phẳng (Q)
b) Hai mặt phẳng (R) và (P) trùng nhau
Cho hai mặt phẳng song song (P) và (Q). Mặt phẳng (R) cắt mặt phẳng (P) theo giao tuyến a.
a) Mặt phẳng (R) có cắt mặt phẳng (Q) theo giao tuyến b, hãy nêu nhận xét về vị trí tương đối giữa hai giao tuyến a và b (Hình 64)
b) Trong trường hợp mặt phẳng (R) cắt mặt phẳng (Q) theo giao tuyến b, hãy nêu nhận xét về vị trí tương đối giữa hai giao tuyến a và b (Hình 64)

Phương pháp giải:
Cho hai mặt phẳng song song (P) và (Q). Nếu mặt phẳng (R) cắt mặt phẳng (P) thì cùng cắt mặt phẳng (Q) và hai giao tuyến của chúng song song với nhau
Lời giải chi tiết:
a) Hai giao tuyến a và b song song với nhau
b) Hai giao tuyến a và b song song với nhau
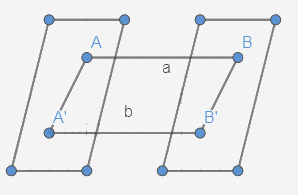
Cho hai mặt phẳng (P) và (Q) song song với nhau. Đường thẳng a cắt hai mặt phẳng trên theo thứ tự tại A, B. Đường thẳng b song song với đường thẳng a và cắt hai mặt phẳng (P) và (Q) lần lượt tại A’, B’. Chứng minh rằng \(AB = A'B'\)
Phương pháp giải:
Hình tứ giác có hai cặp cạnh song song với nhau gọi là hình bình hành.
Lời giải chi tiết:

Ta có (P) // (Q)
Suy ra AA’ // BB’ (1)
Ta có a // b
Suy ra AB // A’B’ (2)
Từ (1) và (2) suy ra AA’B’B là hình bình hành
Do đó AB = A’B’
Mục 2 của chương trình Toán 11 tập 1 - Cánh Diều tập trung vào các kiến thức về hàm số bậc hai. Đây là một phần quan trọng, nền tảng cho các kiến thức toán học nâng cao hơn. Việc nắm vững các khái niệm, định lý và phương pháp giải bài tập trong mục này là vô cùng cần thiết.
Hàm số bậc hai có dạng tổng quát là y = ax² + bx + c, với a ≠ 0. Các yếu tố quan trọng cần nắm vững bao gồm:
Trong mục 2, các bài tập thường tập trung vào các dạng sau:
Phương pháp giải:
Bài 1: (Trang 106) Cho hàm số y = 2x² - 5x + 3. Tìm đỉnh và trục đối xứng của parabol.
Giải:
Hệ số a = 2, b = -5, c = 3.
Hoành độ đỉnh: x₀ = -b/2a = -(-5)/(2*2) = 5/4.
Tung độ đỉnh: y₀ = 2*(5/4)² - 5*(5/4) + 3 = 2*(25/16) - 25/4 + 3 = 25/8 - 50/8 + 24/8 = -1/8.
Vậy đỉnh của parabol là (5/4, -1/8).
Trục đối xứng là đường thẳng x = 5/4.
Bài 2: (Trang 107) Xác định khoảng đồng biến, nghịch biến của hàm số y = -x² + 4x - 1.
Giải:
Hệ số a = -1 < 0, nên hàm số nghịch biến trên khoảng (-∞, 2) và đồng biến trên khoảng (2, +∞).
Bài 3: (Trang 108) Tìm giá trị lớn nhất của hàm số y = -x² + 6x - 5.
Giải:
Hệ số a = -1 < 0, nên hàm số đạt giá trị lớn nhất tại đỉnh của parabol.
Hoành độ đỉnh: x₀ = -6/(2*(-1)) = 3.
Tung độ đỉnh: y₀ = -(3)² + 6*3 - 5 = -9 + 18 - 5 = 4.
Vậy giá trị lớn nhất của hàm số là 4.
Để nắm vững kiến thức về hàm số bậc hai, các em nên luyện tập thêm các bài tập khác trong sách giáo khoa và các tài liệu tham khảo. Đồng thời, hãy tìm hiểu thêm về các ứng dụng của hàm số bậc hai trong thực tế.
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về cách giải các bài tập trong mục 2 trang 106, 107, 108 SGK Toán 11 tập 1 - Cánh Diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!