Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải quyết các bài tập trong mục 3 trang 102 sách giáo khoa Toán 11 tập 2, chương trình Cánh Diều.
Chúng tôi hiểu rằng việc tự học Toán đôi khi gặp nhiều khó khăn. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải chính xác, rõ ràng, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Trong Hình 64, hai mép của con đường gợi nên hình ảnh hai đường thẳng song song (Delta ) và (Delta '). Xét điểm (A) trên đường thẳng (Delta ).
Trong Hình 64, hai mép của con đường gợi nên hình ảnh hai đường thẳng song song \(\Delta \) và \(\Delta '\). Xét điểm \(A\) trên đường thẳng \(\Delta \).
a) Khoảng cách từ điểm \(A\) đến đường thẳng \(\Delta '\) có phụ thuộc vào vị trí của điểm \(A\) trên đường thẳng \(\Delta \) hay không? Vì sao?
b) Khoảng cách đó gợi nên khái niệm gì trong hình học liên quan đến hai đường thẳng song song \(\Delta \) và \(\Delta '\)?
Phương pháp giải:
Sử dụng tính chất của hai đường thẳng song song.
Lời giải chi tiết:
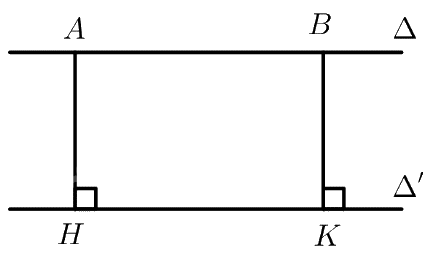
a) Trên đường thẳng \(\Delta \) lấy điểm \(B\) khác \(A\).
Kẻ \(AH \bot \Delta ',BK \bot \Delta '\left( {H,K \in \Delta '} \right)\)
\(ABKH\) là hình chữ nhật \( \Rightarrow AH = BK\)
\( \Rightarrow d\left( {A,\Delta '} \right) = d\left( {B,\Delta '} \right)\)
Vậy khoảng cách từ điểm \(A\) đến đường thẳng \(\Delta '\) không phụ thuộc vào vị trí của điểm \(A\) trên đường thẳng \(\Delta \).
b) Khoảng cách đó gợi nên khái niệm khoảng cách giữa hai đường thẳng song song.
Người ta dựng các cột đèn vuông góc với mặt đường, trong đó mỗi cột đèn gợi nên hình ảnh một đường thẳng. Khoảng cách giữa hai chân cột đèn liên tiếp đo được là 5 m. Tại sao có thể nói khoảng cách giữa hai cột đèn đó là 5 m.
Phương pháp giải:
Dựa vào định nghĩa: Khoảng cách giữa hai đường thẳng song song \(\Delta ,\Delta '\) là khoảng cách từ một điểm bất kì thuộc đường thẳng này đến đường thẳng kia.
Lời giải chi tiết:
Các cột đèn được dựng thẳng đứng và vuông góc với mặt đường thì chúng song song với nhau. Do đó, đoạn thẳng nối hai chân cột chính là khoảng cách giữa hai đường thẳng song song. Vậy ta có thể nói khoảng cách giữa hai cột đèn đó là 5 m.
Mục 3 trang 102 SGK Toán 11 tập 2 - Cánh Diều thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, trước hết, học sinh cần nắm vững lý thuyết liên quan. Điều này bao gồm các định nghĩa, tính chất, định lý và công thức quan trọng. Việc hiểu rõ bản chất của vấn đề sẽ giúp bạn tiếp cận bài toán một cách logic và tìm ra lời giải chính xác.
Thông thường, mục 3 trang 102 SGK Toán 11 tập 2 - Cánh Diều sẽ bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải các bài tập trong mục 3 trang 102 SGK Toán 11 tập 2 - Cánh Diều, chúng tôi sẽ cung cấp lời giải chi tiết cho từng bài tập. Dưới đây là hướng dẫn giải:
Đề bài: (Giả sử đề bài là một bài toán cụ thể).
Lời giải: (Giải thích chi tiết từng bước giải bài toán, sử dụng các công thức và tính chất liên quan. Chú trọng việc giải thích rõ ràng, dễ hiểu để học sinh có thể tự học theo.)
Đề bài: (Giả sử đề bài là một bài toán cụ thể).
Lời giải: (Giải thích chi tiết từng bước giải bài toán, sử dụng các công thức và tính chất liên quan. Chú trọng việc giải thích rõ ràng, dễ hiểu để học sinh có thể tự học theo.)
Để giải các bài tập Toán 11 một cách nhanh chóng và hiệu quả, bạn có thể áp dụng một số mẹo sau:
(Ví dụ về ứng dụng kiến thức trong mục 3 vào giải quyết một bài toán thực tế, ví dụ như tính toán trong kỹ thuật, kinh tế, hoặc các lĩnh vực khác).
Để củng cố kiến thức và kỹ năng giải bài tập, bạn nên luyện tập thêm với các bài tập tương tự trong sách bài tập hoặc các nguồn tài liệu khác. Việc luyện tập thường xuyên sẽ giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Hy vọng rằng, với hướng dẫn chi tiết và các mẹo giải nhanh trên, bạn đã có thể tự tin giải quyết các bài tập trong mục 3 trang 102 SGK Toán 11 tập 2 - Cánh Diều. Chúc bạn học tập tốt và đạt kết quả cao!