Bài học này cung cấp kiến thức nền tảng về hai đường thẳng vuông góc trong chương trình Toán 11 Cánh diều. Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, điều kiện, tính chất và các ứng dụng quan trọng của khái niệm này.
Nội dung được trình bày một cách dễ hiểu, kèm theo ví dụ minh họa và bài tập thực hành để giúp bạn nắm vững lý thuyết và rèn luyện kỹ năng giải toán.
1. Góc giữa hai đường thẳng trong không gian Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b, kí hiệu (a, b) hoặc \(\widehat {(a,b)}\).
1. Góc giữa hai đường thẳng trong không gian
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b, kí hiệu (a, b) hoặc \(\widehat {(a,b)}\).
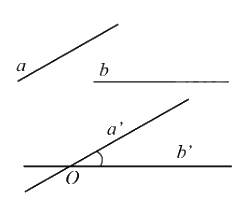
Nhận xét:
- Góc giữa hai đường thẳng a, b không phụ thuộc vào vị trí điểm O. Thông thường, khi tìm góc giữa hai đường thẳng a, b, ta chọn O thuộc a hoặc O thuộc b.
- Góc giữa hai đường thẳng a, b bằng góc giữa hai đường thẳng b, a, tức là (a, b) = (b, a).
- Góc giữa hai đường thẳng không vượt quá \({90^0}\).
- Nếu a // b thì (a, c) = (b, c) với mọi đường thẳng c trong không gian.
2. Hai đường thẳng vuông góc trong không gian
Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng \({90^0}\).
Khi hai đường thẳng a và b vuông góc với nhau, ta kí hiệu \(a \bot b\).
Nhận xét: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.
Trong chương trình Toán 11, đặc biệt là theo sách Cánh diều, kiến thức về hai đường thẳng vuông góc đóng vai trò quan trọng. Nó là nền tảng cho việc hiểu các khái niệm hình học không gian và giải quyết các bài toán liên quan đến vectơ, phương trình đường thẳng và mặt phẳng.
Hai đường thẳng được gọi là vuông góc khi góc giữa chúng bằng 90 độ. Trong mặt phẳng tọa độ, điều kiện để hai đường thẳng (d1) và (d2) vuông góc được xác định thông qua tích vô hướng của hai vectơ chỉ phương của chúng. Cụ thể:
Ngoài ra, nếu một đường thẳng vuông góc với một đường thẳng khác, thì nó cũng vuông góc với mọi đường thẳng song song với đường thẳng đó.
Hai đường thẳng vuông góc có những tính chất quan trọng sau:
Lý thuyết về hai đường thẳng vuông góc có nhiều ứng dụng trong thực tế và trong các bài toán hình học:
Bài tập 1: Cho hai đường thẳng (d1): 2x + y - 3 = 0 và (d2): x - 2y + 1 = 0. Chứng minh rằng (d1) ⊥ (d2).
Giải:
Vectơ chỉ phương của (d1) là u = (1; -2). Vectơ chỉ phương của (d2) là v = (2; 1). Ta có u.v = 1*2 + (-2)*1 = 0. Vậy (d1) ⊥ (d2).
Bài tập 2: Tìm phương trình đường thẳng đi qua điểm A(1; 2) và vuông góc với đường thẳng (d): 3x - y + 5 = 0.
Giải:
Vectơ chỉ phương của (d) là u = (1; 3). Vectơ pháp tuyến của (d) là n = (3; -1). Đường thẳng cần tìm có vectơ chỉ phương là v = n = (3; -1). Phương trình đường thẳng cần tìm là: 3(x - 1) - (y - 2) = 0 ⇔ 3x - y + 1 = 0.
Lý thuyết hai đường thẳng vuông góc liên hệ mật thiết với các kiến thức khác trong hình học như:
Việc nắm vững lý thuyết và rèn luyện kỹ năng giải bài tập về hai đường thẳng vuông góc là bước chuẩn bị quan trọng cho việc học các kiến thức nâng cao hơn trong chương trình Toán 11 và các chương trình học tiếp theo.