Bài 9 trang 21 SGK Toán 11 tập 1 thuộc chương trình học Giải tích của môn Toán lớp 11, tập trung vào việc xét tính đơn điệu của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để xác định khoảng đồng biến, nghịch biến của hàm số, từ đó hiểu rõ hơn về tính chất của hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 9 trang 21 SGK Toán 11 tập 1 - Cánh diều, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12m. Biết rằng hai sợi cáp trên cũng được gắn với mặt đất tại một vị trí cách chân cột 15m (Hình 18)
Đề bài
Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12m. Biết rằng hai sợi cáp trên cũng được gắn với mặt đất tại một vị trí cách chân cột 15m (Hình 18)
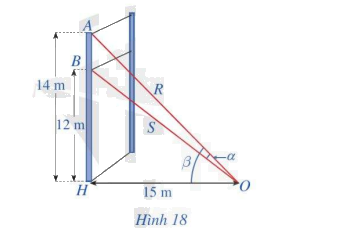
a) Tính \(\tan \alpha \), ở đó \(\alpha \) là góc giữa hai sợi cáp trên
b) Tìm góc \(\alpha \) (làm tròn đến kết quả hàng đơn vị theo đơn vị độ)
Phương pháp giải - Xem chi tiết
Dựa vào công thức cộng để tính
Lời giải chi tiết
a) Ta có:
\(\begin{array}{l}\tan \widehat {AOB} = \frac{{AH}}{{HO}} = \frac{{14}}{{15}}\\\tan \beta = \frac{{BH}}{{HO}} = \frac{{12}}{{15}} = \frac{4}{5}\end{array}\)
Ta có: \(\tan \alpha = \tan \left( {\widehat {AOB} - \beta } \right) = \frac{{\tan \widehat {AOB} - \tan \beta }}{{1 + \tan \widehat {AOB.}\tan \beta }} = \frac{{\frac{{14}}{{15}} - \frac{4}{5}}}{{1 + \frac{{14}}{{15}}.\frac{4}{5}}} = \frac{{10}}{{131}}\)
b) \(\tan \alpha = \frac{{10}}{{131}} \Rightarrow \alpha \approx {4^o}\)
Bài 9 trang 21 SGK Toán 11 tập 1 - Cánh diều yêu cầu xét tính đơn điệu của các hàm số sau:
Để xét tính đơn điệu của hàm số, ta cần tính đạo hàm f'(x):
f'(x) = 6x2 - 6x = 6x(x - 1)
Ta xét dấu f'(x):
Vậy hàm số đồng biến trên các khoảng (-∞; 0) và (1; +∞), nghịch biến trên khoảng (0; 1).
Tính đạo hàm f'(x):
f'(x) = 4x3 - 12x2 + 8x = 4x(x2 - 3x + 2) = 4x(x - 1)(x - 2)
Xét dấu f'(x):
Vậy hàm số đồng biến trên các khoảng (0; 1) và (2; +∞), nghịch biến trên các khoảng (-∞; 0) và (1; 2).
Tính đạo hàm f'(x):
f'(x) = -3x2 + 6x = -3x(x - 2)
Xét dấu f'(x):
Vậy hàm số đồng biến trên khoảng (0; 2), nghịch biến trên các khoảng (-∞; 0) và (2; +∞).
Khi xét tính đơn điệu của hàm số, việc xác định đúng dấu của đạo hàm trên các khoảng là rất quan trọng. Học sinh cần nắm vững các quy tắc xét dấu và áp dụng linh hoạt để giải quyết các bài tập tương tự.
Ngoài ra, việc vẽ đồ thị hàm số cũng giúp học sinh hình dung rõ hơn về tính đơn điệu của hàm số. Sử dụng các công cụ vẽ đồ thị trực tuyến hoặc phần mềm toán học có thể hỗ trợ quá trình này.
Để củng cố kiến thức về xét tính đơn điệu của hàm số, học sinh có thể tự giải các bài tập sau:
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về Bài 9 trang 21 SGK Toán 11 tập 1 - Cánh diều và tự tin giải các bài tập tương tự.