Bài 8 trang 120 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Cánh Diều, tập trung vào việc rèn luyện kỹ năng giải các bài toán về đạo hàm. Bài tập này giúp học sinh hiểu sâu hơn về ý nghĩa và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình lăng trụ tam giác ABC.A’B’C’. Lấy M, M’ lần lượt là trung điểm các đoạn thẳng BC, B’C’; lấy các điểm G, G’, K lần lượt thuộc các đoạn AM, A’M’, A’B sao cho \(\frac{{AG}}{{AM}} = \frac{{A'G'}}{{A'M'}} = \frac{{A'K}}{{A'B}} = \frac{2}{3}\)
Đề bài
Cho hình lăng trụ tam giác ABC.A’B’C’. Lấy M, M’ lần lượt là trung điểm các đoạn thẳng BC, B’C’; lấy các điểm G, G’, K lần lượt thuộc các đoạn AM, A’M’, A’B sao cho \(\frac{{AG}}{{AM}} = \frac{{A'G'}}{{A'M'}} = \frac{{A'K}}{{A'B}} = \frac{2}{3}\)
a) Chứng minh rằng CM’ // (A’BM’)
b) Chứng minh rằng G’K // (BCC’B’)
c) Chứng minh rằng (GG’K) // (BCC’B’)
d) Gọi\(\left( \alpha \right)\)là mặt phẳng đi qua K và song song với mặt phẳng (ABC). Mặt phẳng\(\left( \alpha \right)\)cắt cạnh CC’ tại điểm I. Tính \(\frac{{IC}}{{IC'}}\)
Phương pháp giải - Xem chi tiết
a,b, Đường thẳng d // (P) nếu d //d', d' nằm trong (P).
c, (P)//(Q) nếu d,d' nằm trong (P) và d, d'//(Q).
Lời giải chi tiết
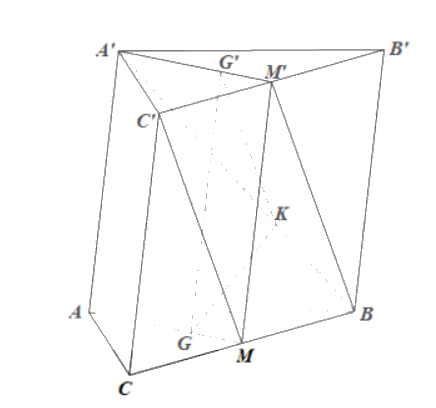
a) Trong mp(BCC’B’) có tứ giác BCC’B’ là hình bình hành nên BC // B’C’ và BC = B’C’.
Lại có M, N lần lượt là trung điểm của BC, B’C’ nên BM = C’M’ = ½ BC = ½ B’C’.
Tứ giác BMC’M’ có BM // C’M’ (do BC // B’C’) và BM = C’M’ nên BMC’M’ là hình bình hành
Do đó C’M // M’B, mà M’B ⊂ (A’BM’) nên C’M // (A’BM’).
b) Trong mp(A’BM’), xét ∆A’BM’ có \(\frac{{A'G'}}{{A'M'}} = \frac{{A'K}}{{A'B}} = \frac{2}{3}\) nên G’K // M’B (theo định lí Thalès đảo)
Mà M’B ⊂ (BCC’B’) nên G’K // (BCC’B’).
c) Trong mp(BCC’B’), tứ giác CMM’C’ có C’M’ // CM và C’M’ = CM = ½ BC = ½ B’C’
Do đó tứ giác CMM’C’ là hình bình hành nên M’M // C’C và M’M = C’C.
Mà A’A // C’C và A’A = C’C nên A’A // M’M và A’A = M’M.
Khi đó AMM’A’ là hình bình hành nên A’M’ // AM và A’M’ = AM.
Lại có\(\frac{{AG}}{{AM}} = \frac{{A'G'}}{{A'M'}} = \frac{2}{3}\) nên A’G’ = AG, do đó G’M’ = GM.
Xét tứ giác GMM’G’ có: G’M’ = GM (do A’M’ // AM) và G’M’ = GM.
Do đó GMM’G’ là hình bình hành nên G’G // M’M
Lại có M’M ⊂ (BCC’B’) nên G’G // (BCC’B’).
Ta có: G’K // (BCC’B’);
G’G // (BCC’B’);
G’K, G’G cắt nhau tại điểm G’ và cùng nằm trong (GG’K)
Do đó (GG’K) // ((BCC’B’).
d) Trong mp(ABB’A’), vẽ đường thẳng qua K và song song với AB, A’B’; cắt A’A và B’B lần lượt tại J và H.
Trong mp (ACC’A”), vẽ đường thẳng qua J và song song với AC, A’C’; cắt C’C tại I.
Ta có: IJ // AC mà AC ⊂ (ABC) nên IJ // (ABC);
JK // AB mà AB ⊂ (ABC) nên JK // (ABC).
Lại có IJ và JK cắt nhau tại J và cùng nằm trong mp(IJK) nên (IJK) // (ABC).
Theo bài, mp(α) // (ABC) và đi qua K nên mp(α) chính là mp(IJK).
Khi đó CC’ cắt (α) tại I.
Ta có: (IJK) // (ABC) mà (ABC) // (A’B’C’) nên (A’B’C’), (IJK), (ABC) là ba mặt phẳng song song với nhau.
Xét hai cát tuyến C’C và A’B bất kì cắt ba mặt phẳng song song (A’B’C’), (IJK), (ABC) lần lượt tại các điểm C’, I, C và A’, K, B. Khi đó theo định lí Thalès trong không gian ta có:\(\frac{{C'I}}{{A'K}} = \frac{{IC}}{{KB}}\)
Suy ra \(\frac{{KB}}{{A'K}} = \frac{{IC}}{{C'I}}\)
Theo bài, \(\frac{{A'K}}{{A'B}} = \frac{2}{3}\) nên \(\frac{{A'B}}{{A'K}} = \frac{3}{2}\) do đó \(\frac{{A'B - A'K}}{{A'K}} = \frac{{3 - 2}}{2}\) hay \(\frac{{KB}}{{A'K}} = \frac{1}{2}\)
Vậy \(\frac{{IC}}{{IC'}} = \frac{{KB}}{{A'K}} = \frac{1}{2}\).
Bài 8 trang 120 SGK Toán 11 tập 1 - Cánh Diều yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến cực trị của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như đạo hàm, điểm cực trị, và các phương pháp tìm cực trị của hàm số.
Bài tập này thường bao gồm các dạng bài sau:
Ví dụ: Tìm cực trị của hàm số f(x) = x3 - 3x2 + 2.
Giải:
Việc giải thành thạo Bài 8 trang 120 SGK Toán 11 tập 1 - Cánh Diều không chỉ giúp học sinh nắm vững kiến thức về đạo hàm và cực trị của hàm số mà còn là nền tảng quan trọng để học tốt các chương trình Toán học nâng cao hơn. Kỹ năng giải bài tập này cũng rất hữu ích trong việc giải quyết các bài toán thực tế trong nhiều lĩnh vực khác nhau.
Giaitoan.edu.vn cung cấp đầy đủ các lời giải chi tiết, bài tập luyện tập và các tài liệu học tập hữu ích khác cho môn Toán 11. Chúng tôi cam kết mang đến cho học sinh một môi trường học tập trực tuyến chất lượng cao, giúp các em học tập hiệu quả và đạt kết quả tốt nhất.