Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong sách giáo khoa Toán 11 tập 1 - Cánh Diều.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt trong môn Toán.
Hình 2 biểu diễn các số hạng của dãy số (left( {{u_n}} right),) với ({u_n} = frac{1}{n}) trên hệ trục tọa độ.
Hình 2 biểu diễn các số hạng của dãy số \(\left( {{u_n}} \right),\) với \({u_n} = \frac{1}{n}\) trên hệ trục tọa độ.
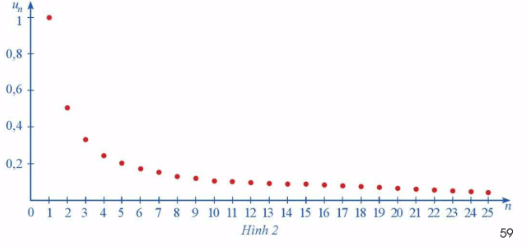
a) Nhận xét về sự thay đổi các giá trị \({u_n}\) khi n ngày càng lớn.
b) Hoàn thành bảng và trả lời câu hỏi sau:

Kể từ số hạng \({u_n}\) nào của dãy số thì khoảng cách từ \({u_n}\) đến 0 nhỏ hơn 0,001? 0,0001?
Phương pháp giải:
Quan sát hình 2 và rút ra nhận xét.
Lời giải chi tiết:
a) Khi n ngày càng lớn thì các giá trị \({u_n}\) ngày càng giảm tiến dần về gần trục Ox.
b)

Kể từ số hạng \({u_{1001}}\) trở đi thì khoảng cách từ \({u_n}\) đến 0 nhỏ hơn 0,001
Kể từ số hạng \({u_{10001}}\) trở đi thì khoảng cách từ \({u_n}\) đến 0 nhỏ hơn 0,0001
Chứng minh rằng:
a) \(\lim 0 = 0;\)
b) \(\lim \frac{1}{{\sqrt n }} = 0.\) \(\)
Phương pháp giải:
Sử dụng định nghĩa dãy số có giới hạn 0.
Dãy số \(\left( {{u_n}} \right)\)có giới hạn 0 khi n dần tới dương vô cực, nếu \(\left| {{u_n}} \right|\) có thể nhỏ hơn một số dương bé tùy ý , kể tử một số hạng nào đó trở đi.
Lời giải chi tiết:
a) Vì \(\left| {{u_n}} \right| = \left| 0 \right| = 0 < 1\) nên theo định nghĩa dãy số có giới hạn 0 ta có \(\lim 0 = 0;\)
b) Vì \(0 < \left| {\frac{1}{{\sqrt n }}} \right| < 1\) nên theo định nghĩa dãy số có giới hạn 0 ta có \(\lim \frac{1}{{\sqrt n }} = 0.\)
Chứng minh rằng \(\lim \frac{{ - 4n + 1}}{n} = - 4.\)
Phương pháp giải:
Sử dụng định nghĩa dãy số có giới hạn hữu hạn.
Dãy số \(\left( {{u_n}} \right)\)có giới hạn là số thực a khi n dần tới dương vô cực, nếu \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - a} \right) = 0\), kí hiệu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a\)hay \({u_n} \to a\)khi \(n \to + \infty \) hay \(\lim {u_n} = a\).
Lời giải chi tiết:
Vì \(\lim \left( {\frac{{ - 4n + 1}}{n} + 4} \right) = \lim \frac{1}{n} = 0\) nên \(\lim \frac{{ - 4n + 1}}{n} = - 4.\)
Chứng minh rằng \(\lim {\left( {\frac{e}{\pi }} \right)^n} = 0.\)
Phương pháp giải:
Dãy số \(\left( {{u_n}} \right)\)có giới hạn 0 khi n dần tới dương vô cực, nếu \(\left| {{u_n}} \right|\) có thể nhỏ hơn một số dư mơng bé tùy ý , kể tử một số hạng nào đó trở đi.
Lời giải chi tiết:
Vì \(\left| {\frac{e}{\pi }} \right| < 1\) nên theo định nghĩa dãy số có giới hạn 0 ta có \(\lim {\left( {\frac{e}{\pi }} \right)^n} = 0.\)
Mục 1 của chương trình Toán 11 tập 1 - Cánh Diều tập trung vào các kiến thức cơ bản về giới hạn của hàm số. Đây là nền tảng quan trọng để học sinh hiểu rõ hơn về đạo hàm và tích phân trong các chương tiếp theo. Việc nắm vững các khái niệm và phương pháp giải bài tập trong mục này là vô cùng cần thiết.
Các bài tập trên trang 59 tập trung vào việc kiểm tra sự hiểu biết của học sinh về định nghĩa giới hạn. Để giải các bài tập này, học sinh cần:
Trang 60 giới thiệu các bài tập về giới hạn của hàm số khi x tiến tới vô cùng. Các phương pháp giải thường được sử dụng bao gồm:
Các bài tập trên trang 61 và 62 là sự kết hợp của các kiến thức đã học, đòi hỏi học sinh phải vận dụng linh hoạt các phương pháp giải khác nhau. Một số dạng bài tập thường gặp bao gồm:
Để giải các bài tập về giới hạn một cách hiệu quả, học sinh nên:
Học Toán 11 đòi hỏi sự kiên trì và nỗ lực. Hãy dành thời gian ôn tập lý thuyết, làm bài tập và tìm hiểu các phương pháp giải khác nhau. Đừng ngần ngại hỏi thầy cô hoặc bạn bè nếu gặp khó khăn. Chúc các em học tập tốt!
| Bài tập | Phương pháp giải |
|---|---|
| Bài 1 trang 59 | Áp dụng định nghĩa giới hạn |
| Bài 2 trang 60 | Chia tử và mẫu cho x^2 |
| Bài 3 trang 61 | Sử dụng giới hạn đặc biệt |