Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 tập 2. Bài viết này sẽ hướng dẫn bạn giải các bài tập trong mục 2 trang 30 và 31 của sách giáo khoa Toán 11 tập 2 - Cánh Diều.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải một cách cẩn thận, kèm theo các giải thích rõ ràng để giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Xét số vô tỉ: (sqrt 2 = 1,4142135624...). Xét dãy số hữu tỉ: ({r_1} = 1;{r_2} = 1,4;{r_3} = 1,41;{r_4} = 1,414;{r_5} = 1,4142;{r_6} = 1,41421;...)
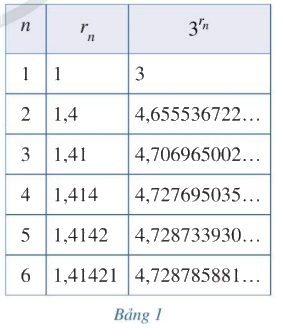
Xét số vô tỉ: \(\sqrt 2 = 1,4142135624...\). Xét dãy số hữu tỉ: \({r_1} = 1;{r_2} = 1,4;{r_3} = 1,41;{r_4} = 1,414;{r_5} = 1,4142;{r_6} = 1,41421;...\) và \(\lim {r_n} = \sqrt 2 \). Bằng cách tính \({3^{{r_n}}}\) tương ứng, ta nhận được Bảng 1 ghi các dãy số \(\left( {{r_n}} \right)\) và \(\left( {{3^{{r_n}}}} \right)\) với n = 1, 2, …, 6. Người ta chứng minh được rằng khi \(n \to + \infty \) thì dãy số \(\left( {{3^{{r_n}}}} \right)\) dần đến một giới hạn mà ta gọi là \({3^{\sqrt 2 }}\). Nêu dự đoán về giá trị của số \({3^{\sqrt 2 }}\) (đến hàng phần trăm).
Phương pháp giải:
Dựa vào giới hạn của dãy số hữu tỉ để dự đoán
Lời giải chi tiết:
Do \({r_1} = 1;{r_2} = 1,4;{r_3} = 1,41;{r_4} = 1,414;{r_5} = 1,4142;{r_6} = 1,41421;...\) => \({3^{\sqrt 2 }} \approx 1,41\)
So sánh \({10^{\sqrt 2 }}\,\,và \,\,10\)
Phương pháp giải:
Dựa vào dự đoán ở ví dụ 5 để so sánh
Lời giải chi tiết:
Do \({10^{\sqrt 2 }} \approx 25,95 > 10 \Rightarrow {10^{\sqrt 2 }} > 10\)
Nêu những tính chất của phép tính lũy thừa với số mũ nguyên của một số thực dương
Phương pháp giải:
Dựa vào các kiến thức đã học về lũy thừa ở cấp 2 để làm bài
Lời giải chi tiết:
+ \({a^\alpha }.{a^\beta } = {a^{\alpha + \beta }}\)
+ \(\frac{{{a^\alpha }}}{{{a^\beta }}} = {a^{\alpha - \beta }}\)
+ \({\left( {{a^\alpha }} \right)^\beta } = {a^{\alpha .\beta }}\)
+ \({(ab)^\alpha } = {a^\alpha }.{b^\alpha }\)
+ \({\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{{{b^\alpha }}}\)
+ Nếu a > 1 thì \({a^\alpha } > {a^\beta } \Leftrightarrow \alpha < \beta \)
+ Nếu 0 < a < 1 thì \({a^\alpha } > {a^\beta } \Leftrightarrow \alpha > \beta \)
Không sử dụng máy tính cầm tay, hãy so sánh các số: \({2^{2\sqrt 3 }}\,\,và \,\,{2^{3\sqrt 2 }}\)
Phương pháp giải:
Dựa vào Ví dụ 7 để làm
Lời giải chi tiết:
Ta có:
\(\left. \begin{array}{l}{\left( {2\sqrt 3 } \right)^2} = 12\\{\left( {3\sqrt 2 } \right)^2} = 18\end{array} \right\} \Rightarrow 2\sqrt 3 < 3\sqrt 2 \Rightarrow {2^{2\sqrt 3 }} < {2^{3\sqrt 2 }}\)
Dùng máy tính cầm tay để tính (làm tròn kết quả đến hàng phần trăm):
a) \( (-2,7)^{-4}\);
b) \( \sqrt 3 - 1)^{\sqrt[3] {4} + 1}\)
Phương pháp giải:
Sử dụng máy tính để tính, làm tròn đến hàng phần trăm.
Lời giải chi tiết:
a) \( (-2,7)^{-4} \approx 0,02\);
b) \( \sqrt 3 - 1)^{\sqrt[3] {4} + 1} \approx 0,45\)
Mục 2 của SGK Toán 11 tập 2 - Cánh Diều tập trung vào các kiến thức về phép biến hình. Cụ thể, các bài tập trang 30 và 31 xoay quanh việc xác định các phép biến hình, tính chất của chúng và ứng dụng trong giải quyết các bài toán hình học.
Đề bài: Cho điểm A(1; 2). Tìm ảnh của điểm A qua phép tịnh tiến theo vectơ v = (3; -1).
Lời giải: Gọi A'(x'; y') là ảnh của điểm A qua phép tịnh tiến theo vectơ v. Khi đó, ta có:
x' = x + vx = 1 + 3 = 4
y' = y + vy = 2 + (-1) = 1
Vậy, A'(4; 1).
Đề bài: Cho đường thẳng d: x + y - 2 = 0. Tìm ảnh của đường thẳng d qua phép đối xứng trục Ox.
Lời giải: Gọi d' là ảnh của đường thẳng d qua phép đối xứng trục Ox. Khi đó, d' có phương trình:
x - y - 2 = 0
Đề bài: Cho đường tròn (C): (x - 1)^2 + (y + 2)^2 = 4. Tìm ảnh của đường tròn (C) qua phép đối xứng tâm O.
Lời giải: Gọi (C') là ảnh của đường tròn (C) qua phép đối xứng tâm O. Khi đó, (C') có phương trình:
(x + 1)^2 + (y - 2)^2 = 4
Đề bài: Cho điểm A(2; 3). Tìm ảnh của điểm A qua phép quay tâm O, góc 90 độ.
Lời giải: Gọi A'(x'; y') là ảnh của điểm A qua phép quay tâm O, góc 90 độ. Khi đó, ta có:
x' = -y = -3
y' = x = 2
Vậy, A'(-3; 2).
Để nắm vững kiến thức về phép biến hình, bạn nên luyện tập thêm các bài tập khác trong SGK và các tài liệu tham khảo. Ngoài ra, bạn có thể tìm kiếm các bài giảng online hoặc tham gia các khóa học toán online để được hướng dẫn chi tiết hơn.
Hãy đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Vẽ hình minh họa để hình dung rõ hơn về bài toán. Sử dụng các công thức và tính chất đã học để giải quyết bài toán. Kiểm tra lại kết quả để đảm bảo tính chính xác.