Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 91, 92, 93 sách giáo khoa Toán 11 tập 2 - Cánh Diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho góc nhị diện có hai mặt là hai nửa mặt phẳng (left( P right),left( Q right)) và cạnh của góc nhị diện là đường thẳng (d).
Quan sát hình ảnh một quyển sổ được mở ra (Hình 35), mỗi trang sổ gợi nên hình ảnh của một nửa mặt phẳng. Nêu đặc điểm của hai nửa mặt phẳng đó.
Phương pháp giải:
Dựa vào khái niệm góc nhị diện.
Lời giải chi tiết:
Hai nửa mặt phẳng đó có chung bờ là đường thẳng chứa gáy sổ.
Cho góc nhị diện có hai mặt là hai nửa mặt phẳng \(\left( P \right),\left( Q \right)\) và cạnh của góc nhị diện là đường thẳng \(d\).
Qua một điểm \(O\) trên đường thẳng \(d\), ta kẻ hai tia \(Ox,Oy\) lần lượt thuộc hai nửa mặt phẳng \(\left( P \right),\left( Q \right)\) và cùng vuông góc với đường thẳng \(d\). Góc \(xOy\) gọi là góc phẳng nhị diện của góc nhị diện đã cho (Hình 38).
Giả sử góc \(x'Oy'\) cũng là góc phẳng nhị diện của góc nhị diện đã cho với \(O'\) khác \(O\) (Hình 39).
Hãy so sánh số đo của hai góc \(xOy\) và \(x'Oy'\).

Phương pháp giải:
Sử dụng quan hệ giữa hai đường thẳng song song.
Lời giải chi tiết:
Trong \(\left( P \right)\) ta có:
\(\left. \begin{array}{l}Ox \bot d\\O'x' \bot d\end{array} \right\} \Rightarrow Ox\parallel O'x'\)
Trong \(\left( Q \right)\) ta có:
\(\left. \begin{array}{l}Oy \bot d\\O'y' \bot d\end{array} \right\} \Rightarrow Oy\parallel O'y'\)
Vậy \(\left( {Ox,Oy} \right) = \left( {O'x',O'y'} \right)\) hay số đo của hai góc \(xOy\) và \(x'Oy'\) bằng nhau.
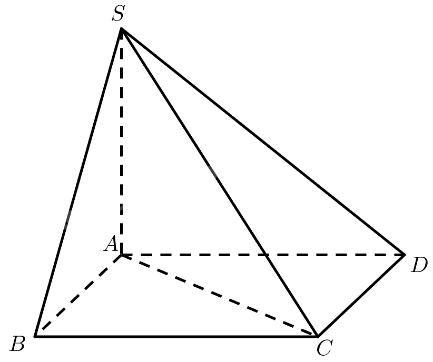
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông và \(SA \bot \left( {ABCD} \right)\). Tính số đo theo đơn vị độ của góc nhị diện:
a) \(\left[ {B,SA,D} \right]\);
b) \(\left[ {B,SA,C} \right]\).
Phương pháp giải:
‒ Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)
Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).
Bước 2: Tìm mặt phẳng \(\left( R \right) \supset c\).
Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).
Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).
Lời giải chi tiết:

a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{D}}\)
Vậy \(\widehat {BA{\rm{D}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,D} \right]\)
\(ABCD\) là hình vuông \( \Rightarrow \widehat {BA{\rm{D}}} = {90^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,D} \right]\) bằng \({90^ \circ }\).
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{C}}\)
Vậy \(\widehat {BA{\rm{C}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,C} \right]\)
\(ABCD\) là hình vuông \( \Rightarrow \widehat {BA{\rm{C}}} = {45^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,C} \right]\) bằng \({45^ \circ }\).
Trong không gian cho hai mặt phẳng \((\alpha), (\beta)\) cắt nhau theo giao tuyến d. Hai mặt phẳng \((\alpha), (\beta)\) tạo nên bao nhiêu góc nhị diện có cạnh của góc nhị diện là đường thẳng d?
Phương pháp giải:
Dựa vào kiến thức về góc nhị diện.
Lời giải chi tiết:
Số góc nhị diện mà hai mặt phẳng (a) và (B) tạo ra bằng số điểm trên đường thẳng d.
Mục 2 của chương trình Toán 11 tập 2 - Cánh Diều tập trung vào các kiến thức về đường thẳng và mặt phẳng trong không gian. Các bài tập trang 91, 92, 93 thường xoay quanh việc xác định vị trí tương đối giữa đường thẳng và mặt phẳng, tìm giao điểm, góc giữa chúng, và ứng dụng các định lý liên quan.
Bài tập này yêu cầu học sinh vận dụng các kiến thức về vectơ chỉ phương của đường thẳng và vectơ pháp tuyến của mặt phẳng để xét xem đường thẳng song song, nằm trong mặt phẳng, cắt mặt phẳng hay vuông góc với mặt phẳng. Việc hiểu rõ các điều kiện song song, vuông góc, cắt nhau là rất quan trọng để giải quyết bài toán này.
Để tìm giao điểm của đường thẳng và mặt phẳng, ta cần giải hệ phương trình bao gồm phương trình tham số của đường thẳng và phương trình của mặt phẳng. Nghiệm của hệ phương trình chính là tọa độ của giao điểm.
Ví dụ: Cho đường thẳng d: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P): x + y - z = 0. Thay phương trình tham số của d vào phương trình (P), ta được: (1 + t) + (2 - t) - (3 + 2t) = 0 => 0 - 2t = 0 => t = 0. Thay t = 0 vào phương trình tham số của d, ta được giao điểm I(1, 2, 3).
Góc giữa đường thẳng và mặt phẳng được tính bằng góc giữa đường thẳng và hình chiếu của nó lên mặt phẳng. Công thức tính góc α là: sin(α) = |cos(θ)|, trong đó θ là góc giữa vectơ chỉ phương của đường thẳng và vectơ pháp tuyến của mặt phẳng.
Lưu ý: Luôn đảm bảo rằng góc α nằm trong khoảng [0, 90°].
Để giải các bài tập về đường thẳng và mặt phẳng một cách hiệu quả, các em cần:
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 2 trang 91, 92, 93 SGK Toán 11 tập 2 - Cánh Diều. Chúc các em học tập tốt và đạt kết quả cao!
| Bài tập | Nội dung chính |
|---|---|
| Bài 1 | Xác định vị trí tương đối giữa đường thẳng và mặt phẳng |
| Bài 2 | Tìm giao điểm của đường thẳng và mặt phẳng |
| Bài 3 | Tính góc giữa đường thẳng và mặt phẳng |