Bài 5 trang 104 SGK Toán 11 tập 1 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 5 trang 104 SGK Toán 11 tập 1 - Cánh Diều, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi M, N lần lượt là trọng tâm của hai tam giác ABF và ABC. Chứng minh rằng đường thẳng MN song song với mặt phẳng (ACF).
Đề bài
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi M, N lần lượt là trọng tâm của hai tam giác ABF và ABC. Chứng minh rằng đường thẳng MN song song với mặt phẳng (ACF).
Phương pháp giải - Xem chi tiết
Dùng định lí Thales đảo và tính chất đường trung bình tam giác.
Lời giải chi tiết
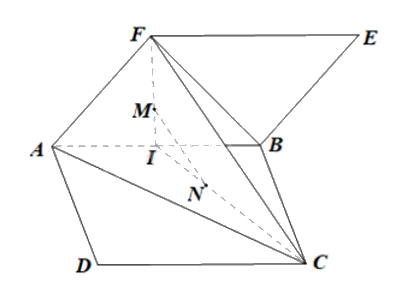
Gọi I là trung điểm của AB.
M là trọng tâm tam giác ABF suy ra \(\frac{{IM}}{{IF}} = \frac{1}{3}\).
N là trọng tâm tam giác ABC suy ra \(\frac{{IN}}{{IC}} = \frac{1}{3}\).
Xét tam giác ICF có \(\frac{{IM}}{{IF}} = \frac{{IN}}{{IC}} = \frac{1}{3}\) suy ra MN//FC (định lí Thales đảo).
Mà FC thuộc mặt phẳng (AFC) suy ra MN//(AFC).
Bài 5 trang 104 SGK Toán 11 tập 1 - Cánh Diều thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Dưới đây là nội dung chi tiết của Bài 5 trang 104 SGK Toán 11 tập 1 - Cánh Diều:
Bài 5 yêu cầu học sinh tính đạo hàm của các hàm số sau:
1. Giải f(x) = 3x2 - 5x + 2
Áp dụng quy tắc tính đạo hàm của tổng và hiệu, ta có:
f'(x) = (3x2)' - (5x)' + (2)'
f'(x) = 6x - 5 + 0
f'(x) = 6x - 5
2. Giải g(x) = x3 + 2x2 - x - 1
Áp dụng quy tắc tính đạo hàm của tổng và hiệu, ta có:
g'(x) = (x3)' + (2x2)' - (x)' - (1)'
g'(x) = 3x2 + 4x - 1 - 0
g'(x) = 3x2 + 4x - 1
3. Giải h(x) = (x2 + 1)(x - 2)
Áp dụng quy tắc tính đạo hàm của tích, ta có:
h'(x) = (x2 + 1)'(x - 2) + (x2 + 1)(x - 2)'
h'(x) = (2x)(x - 2) + (x2 + 1)(1)
h'(x) = 2x2 - 4x + x2 + 1
h'(x) = 3x2 - 4x + 1
4. Giải k(x) = \frac{x + 1}{x - 1}
Áp dụng quy tắc tính đạo hàm của thương, ta có:
k'(x) = \frac{(x + 1)'(x - 1) - (x + 1)(x - 1)'}{(x - 1)^2}
k'(x) = \frac{1(x - 1) - (x + 1)(1)}{(x - 1)^2}
k'(x) = \frac{x - 1 - x - 1}{(x - 1)^2}
k'(x) = \frac{-2}{(x - 1)^2}
Vậy, đạo hàm của các hàm số đã cho là:
Hy vọng lời giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về cách tính đạo hàm của các hàm số và tự tin giải các bài tập tương tự.
Để học thêm về đạo hàm và các kiến thức Toán 11 khác, hãy truy cập giaitoan.edu.vn để được hỗ trợ tốt nhất.