Chào mừng bạn đến với bài học về Lý thuyết Đường thẳng vuông góc với mặt phẳng trong chương trình Toán 11 Cánh diều. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về mối quan hệ giữa đường thẳng và mặt phẳng trong không gian.
Chúng ta sẽ cùng nhau tìm hiểu các định nghĩa, tính chất, dấu hiệu nhận biết và ứng dụng của đường thẳng vuông góc với mặt phẳng.
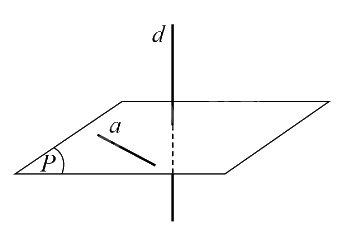
1. Định nghĩa Đường thẳng d được gọi là vuông góc với mặt phẳng (P) nếu đường thẳng d vuông góc với mọi đường thẳng a nằm trong mặt phẳng (P), kí hiệu \(d \bot \left( P \right)\) hoặc \(\left( P \right) \bot d\).
1. Định nghĩa
Đường thẳng d được gọi là vuông góc với mặt phẳng (P) nếu đường thẳng d vuông góc với mọi đường thẳng a nằm trong mặt phẳng (P), kí hiệu \(d \bot \left( P \right)\) hoặc \(\left( P \right) \bot d\).
2. Điều kiện để đường thẳng vuông góc với mặt phẳng
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
Nhận xét: Ta có thể chứng minh hai đường thẳng vuông góc bằng cách chứng minh một đường thẳng vuông góc với một mặt phẳng chứa đường thẳng kia.
3. Tính chất
- Tính chất 1: Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
- Tính chất 2: Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
4. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng
- Tính chất 3:
Cho hai đường thẳng song song. Một mặt phẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
- Tính chất 4:
Cho hai mặt phẳng song song. Một đường thẳng vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.
Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
5. Phép chiếu vuông góc
Cho mặt phẳng (P) và một điểm M tuỳ ý trong không gian. Lấy đường thẳng d đi qua M và vuông góc với (P), gọi giao điểm của d và (P) là M’. Điểm M’ gọi là hình chiếu vuông góc (hay hình chiếu) của điểm M trên (P).
Cho mặt phẳng (P). Quy tắc đặt tương ứng mỗi điểm M trong không gian với hình chiếu vuông góc M’ của điểm đó lên mặt phẳng (P) được gọi là phép chiếu vuông góc lên mặt phẳng (P).
Nhận xét: Vì phép chiếu vuông góc là một trường hợp đặc biệt của phép chiếu song song (khi phương chiếu vuông góc với mặt phẳng chiếu) nên phép chiếu vuông góc có đầy đủ các tính chất của phép chiếu song song.
6. Định lí ba đường vuông góc
Cho đường thẳng a không vuông góc với mặt phẳng (P) và đường thẳng d nằm trong mặt phẳng (P). Khi đó, d vuông góc với a khi và chỉ khi d vuông góc với hình chiếu a’ của a trên (P).
Trong chương trình Hình học không gian lớp 11, kiến thức về đường thẳng vuông góc với mặt phẳng đóng vai trò then chốt. Việc nắm vững lý thuyết này không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng cho các kiến thức nâng cao hơn.
Một đường thẳng được gọi là vuông góc với một mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó. Điều kiện để đường thẳng d vuông góc với mặt phẳng (P) là d vuông góc với hai đường thẳng bất kỳ trong (P).
Có nhiều dấu hiệu để nhận biết một đường thẳng vuông góc với một mặt phẳng. Một số dấu hiệu quan trọng bao gồm:
Đường thẳng vuông góc với mặt phẳng là đường ngắn nhất nối một điểm trên mặt phẳng đến mặt phẳng đó. Đường thẳng nối một điểm trên mặt phẳng với hình chiếu của nó trên mặt phẳng là đường xiên. Độ dài đường xiên luôn lớn hơn độ dài đường vuông góc.
Lý thuyết về đường thẳng vuông góc với mặt phẳng được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến hình học không gian. Ví dụ, để chứng minh một đường thẳng vuông góc với một mặt phẳng, ta có thể sử dụng các dấu hiệu nhận biết đã học. Để tính khoảng cách từ một điểm đến một mặt phẳng, ta thường sử dụng đường vuông góc.
Bài tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD). Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
Hướng dẫn: Kẻ AH vuông góc với SC. Chứng minh AH vuông góc với (ABCD). Tính AH và SC để tìm góc cần tìm.
Bài tập 2: Cho hình hộp chữ nhật ABCD.A'B'C'D'. Chứng minh rằng đường chéo AC' vuông góc với mặt phẳng (ABCD).
Hướng dẫn: Sử dụng tính chất của hình hộp chữ nhật và các dấu hiệu nhận biết đường thẳng vuông góc với mặt phẳng.
Ngoài lý thuyết cơ bản, học sinh có thể tìm hiểu thêm về các ứng dụng của đường thẳng vuông góc với mặt phẳng trong thực tế, ví dụ như trong kiến trúc, xây dựng, hoặc trong việc giải các bài toán tối ưu.
Việc luyện tập thường xuyên với các bài tập đa dạng sẽ giúp học sinh nắm vững kiến thức và kỹ năng giải quyết các bài toán liên quan đến đường thẳng vuông góc với mặt phẳng.
Hy vọng bài học này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin hơn trong việc học tập môn Toán 11.