Bài 1 trang 14 SGK Toán 11 tập 2 thuộc chương trình Toán 11 Cánh Diều, tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số lượng giác, đồ thị hàm số lượng giác và các phép biến đổi lượng giác để giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 1 trang 14, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Mẫu số liệu dưới đây ghi lại tốc độ của 40 ô tô khi đi qua một trạm đo tốc độ (đơn vị: km/h):
Đề bài
Mẫu số liệu dưới đây ghi lại tốc độ của 40 ô tô khi đi qua một trạm đo tốc độ (đơn vị: km/h):

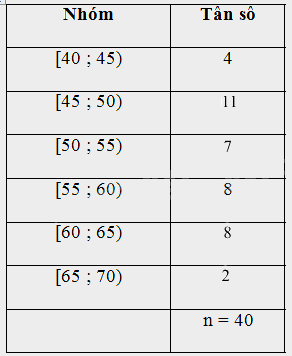
a) Lập bảng tần số ghép nhóm cho mẫu số liệu trên có sáu nhóm ứng với sáu nửa khoảng:
[40 ; 45); [45 ; 50); [50 ; 55); [55 ; 60); [60 ; 65): [65 ; 70)
b) Xác định số trung bình cộng, trung vị, tứ phân vị của mẫu số liệu ghép nhóm trên.
c) Mốt của mẫu số liệu ghép nhóm trên là bao nhiêu?
Phương pháp giải - Xem chi tiết
- Lần lượt đếm số lượng của từng nhóm để lập bảng
- Áp dụng các công thức vừa được học để xác định các đại lượng tiêu biểu
Lời giải chi tiết
a) Bảng tần số ghép nhóm cho mẫu số liệu trên có sáu nhóm ứng với sáu nửa khoảng:
a) Bảng tần số ghép nhóm bao gồm giá trị đại diện và tần số tích lũy:
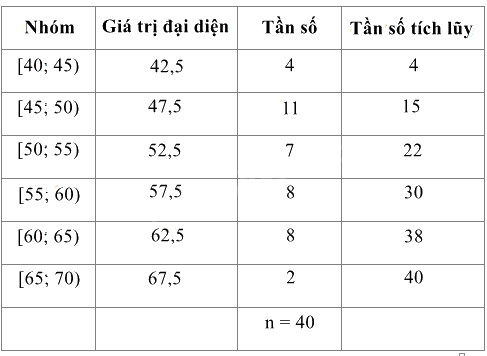
Số phần tử của mẫu là: n = 40
Các đại lượng:
- Số trung bình cộng:
\(\overline x = \frac{{42,5.4 + 47,5.11 + 52,5.7 + 57,5.8 + 62,5.8 + 67,5.2}}{{40}} = 53,875\)
- Trung vị:
\({M_e} = r + \left( {\frac{{\frac{n}{2} - c{f_{k - 1}}}}{{{n_k}}}} \right).d = 50 + \left( {\frac{{\frac{40}{2} - 15}}{7}} \right).5 \approx 53,6\)
- Tứ phân vị:
+ Tứ phân vị thứ hai: \({Q_2} = {M_e} \approx 53,6\)
+ Tứ phân vị thứ nhất:
\({Q_1} = s + \left( {\frac{{\frac{n}{4} - c{f_{p - 1}}}}{{{n_p}}}} \right).h = 45 + \left( {\frac{{\frac{40}{4} - 4}}{{11}}} \right).5 \approx 47,7\)
+ Tứ phân vị thứ ba:
\(Q = t + \left( {\frac{{\frac{{3n}}{4} - c{f_{q - 1}}}}{{{n_q}}}} \right).l = 55 + \left( {\frac{{\frac{3.40}{4} - 22}}{8}} \right).5 = 60\)
b) Mốt của mẫu số liệu:
\({M_o} = u + \left( {\frac{{{n_i} - {n_{i - 1}}}}{{2{n_i} - {n_{i - 1}} - {n_{i + 1}}}}} \right).g = 45 + \left( {\frac{{11 - 4}}{{2.11 - 4 - 7}}} \right).5 \approx 48,2\)
Bài 1 trang 14 SGK Toán 11 tập 2 Cánh Diều yêu cầu học sinh thực hiện các phép tính liên quan đến hàm số lượng giác. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập. (Giả sử bài tập có nhiều phần, mỗi phần sẽ được giải thích chi tiết)
Yêu cầu: Tính giá trị của biểu thức A = sin(30°) + cos(60°).
Giải:
Ta có: sin(30°) = 1/2 và cos(60°) = 1/2. Do đó, A = 1/2 + 1/2 = 1.
Yêu cầu: Tìm tập xác định của hàm số y = tan(x).
Giải:
Hàm số y = tan(x) = sin(x)/cos(x) xác định khi và chỉ khi cos(x) ≠ 0. Điều này tương đương với x ≠ π/2 + kπ, với k là số nguyên.
Để củng cố kiến thức và kỹ năng giải toán, học sinh có thể tự giải các bài tập tương tự sau:
Ngoài SGK Toán 11 tập 2 Cánh Diều, học sinh có thể tham khảo thêm các tài liệu sau:
Bài 1 trang 14 SGK Toán 11 tập 2 Cánh Diều là một bài tập quan trọng giúp học sinh ôn tập và củng cố kiến thức về hàm số lượng giác. Bằng cách nắm vững các kiến thức cơ bản và luyện tập thường xuyên, học sinh có thể giải quyết bài tập này một cách dễ dàng và hiệu quả.