Bài 5 trang 116 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Cánh Diều, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến đạo hàm của hàm số. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức về các quy tắc tính đạo hàm và áp dụng chúng một cách linh hoạt.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 5 trang 116, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Cho tứ diện \(OABC\) thoả mãn \(OA = a,OB = b,OC = c,\) \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {90^ \circ }\)
Đề bài
Cho tứ diện \(OABC\) thoả mãn \(OA = a,OB = b,OC = c,\) \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {90^ \circ }\). Thể tích của khối tứ diện \(OABC\) bằng:
A. \(abc\).
B. \(\frac{{abc}}{2}\).
C. \(\frac{{abc}}{3}\).
D. \(\frac{{abc}}{6}\).
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\).
Lời giải chi tiết
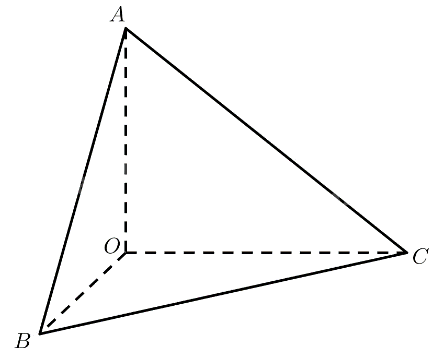
\(\left. \begin{array}{l}\widehat {AOB} = {90^ \circ } \Rightarrow OA \bot OB\\\widehat {COA} = {90^ \circ } \Rightarrow OA \bot OC\end{array} \right\} \Rightarrow OA \bot \left( {OBC} \right)\)
\(\begin{array}{l}{S_{\Delta OBC}} = \frac{1}{2}OB.OC = \frac{1}{2}bc,h = OA = a\\ \Rightarrow {V_{OABC}} = \frac{1}{3}{S_{\Delta OBC}}.OA = \frac{1}{3}.\frac{1}{2}bc.a = \frac{{abc}}{6}\end{array}\)
Chọn D.
Bài 5 trang 116 SGK Toán 11 tập 2 - Cánh Diều yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, trước hết cần nắm vững các khái niệm cơ bản về đạo hàm, bao gồm đạo hàm của hàm số tại một điểm, đạo hàm của hàm số trên một khoảng, và các quy tắc tính đạo hàm (quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp).
Để tính đạo hàm của hàm số f(x) = x^3 - 3x^2 + 2x - 5, ta áp dụng quy tắc tính đạo hàm của tổng và quy tắc tính đạo hàm của lũy thừa:
Do đó, f'(x) = 3x^2 - 6x + 2.
Để tính đạo hàm của hàm số g(x) = (x^2 + 1)(x - 2), ta áp dụng quy tắc tính đạo hàm của tích:
(uv)' = u'v + uv'
Trong đó, u = x^2 + 1 và v = x - 2.
Ta có: u' = 2x và v' = 1.
Do đó, g'(x) = 2x(x - 2) + (x^2 + 1)(1) = 2x^2 - 4x + x^2 + 1 = 3x^2 - 4x + 1.
Để tính đạo hàm của hàm số h(x) = (2x + 3)/(x - 1), ta áp dụng quy tắc tính đạo hàm của thương:
(u/v)' = (u'v - uv')/v^2
Trong đó, u = 2x + 3 và v = x - 1.
Ta có: u' = 2 và v' = 1.
Do đó, h'(x) = (2(x - 1) - (2x + 3)(1))/(x - 1)^2 = (2x - 2 - 2x - 3)/(x - 1)^2 = -5/(x - 1)^2.
Để tính đạo hàm của hàm số k(x) = sin(x) + cos(x), ta áp dụng quy tắc tính đạo hàm của tổng và đạo hàm của các hàm lượng giác:
Do đó, k'(x) = cos(x) - sin(x).
Việc giải Bài 5 trang 116 SGK Toán 11 tập 2 - Cánh Diều đòi hỏi sự nắm vững các quy tắc tính đạo hàm và khả năng áp dụng chúng một cách linh hoạt. Để đạt kết quả tốt, học sinh nên luyện tập thường xuyên và tham khảo các tài liệu hỗ trợ học tập.
Ngoài ra, cần chú ý đến việc kiểm tra lại kết quả sau khi tính đạo hàm để đảm bảo tính chính xác. Việc sử dụng các công cụ tính đạo hàm trực tuyến có thể giúp kiểm tra kết quả một cách nhanh chóng và hiệu quả.
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ tự tin hơn trong việc giải Bài 5 trang 116 SGK Toán 11 tập 2 - Cánh Diều và các bài tập tương tự.