Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 97, 98, 99 sách giáo khoa Toán 11 tập 2 - Cánh Diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho hình chóp \(S.OAB\) thoả mãn \(\left( {AOS} \right) \bot \left( {AOB} \right)\)
Cho hình chóp \(S.OAB\) thoả mãn \(\left( {AOS} \right) \bot \left( {AOB} \right)\), \(\widehat {AOS} = \widehat {AOB} = {90^ \circ }\) (Hình 51).
a) Giao tuyến của hai mặt phẳng \(\left( {AOS} \right)\) và \(\left( {AOB} \right)\) là đường thẳng nào?
b) \(SO\) có vuông góc với giao tuyến của hai mặt phẳng \(\left( {AOS} \right)\) và \(\left( {AOB} \right)\) hay không?
c) \(SO\) có vuông góc với mặt phẳng \(\left( {AOB} \right)\) hay không?
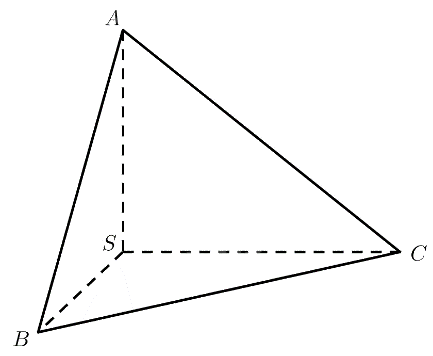
Phương pháp giải:
‒ Để tìm giao tuyến của hai mặt phẳng, ta có 2 cách:
+ Cách 1: Tìm 2 điểm chung phân biệt. Giao tuyến là đường thẳng đi qua hai điểm chung.
+ Cách 2: Tìm 1 điểm chung và 2 đường thẳng song song nằm trên mỗi mặt phẳng. Giao tuyến là đường thẳng đi qua điểm chung và song song với hai đường thẳng đó.
‒ Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
Lời giải chi tiết:
a) Ta có:
\(\left. \begin{array}{l}A \in \left( {AOS} \right) \cap \left( {AOB} \right)\\O \in \left( {AOS} \right) \cap \left( {AOB} \right)\end{array} \right\} \Rightarrow AO = \left( {AOS} \right) \cap \left( {AOB} \right)\)
b) \(\widehat {AOS} = {90^ \circ } \Rightarrow SO \bot AO\)
Vậy \(SO\) có vuông góc với giao tuyến của hai mặt phẳng \(\left( {AOS} \right)\) và \(\left( {AOB} \right)\).
c) \(\widehat {AOS} = {90^ \circ } \Rightarrow SO \bot AO\)
\(\widehat {AOB} = {90^ \circ } \Rightarrow AO \bot BO\)
Vậy \(\widehat {SOB}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {S,AO,B} \right]\)
Vì \(\left( {AOS} \right) \bot \left( {AOB} \right)\) nên \(\widehat {SOB} = {90^ \circ }\)
\(\left. \begin{array}{l} \Rightarrow SO \bot OB\\SO \bot OA\end{array} \right\} \Rightarrow SO \bot \left( {AOB} \right)\)
Cho tứ diện \(ABCD\) có \(\left( {ABD} \right) \bot \left( {BCD} \right)\) và \(CD \bot BD\). Chứng minh rằng tam giác \(ACD\) vuông.
Phương pháp giải:
Sử dụng định lí 2: Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường nào nằm trong mặt phẳng này và vuông góc với giao tuyến cũng vuông góc với mặt phẳng kia.
Lời giải chi tiết:

Ta có:
\(\left. \begin{array}{l}\left( {ABD} \right) \bot \left( {BCD} \right)\\\left( {ABD} \right) \cap \left( {BCD} \right) = BD\\C{\rm{D}} \subset \left( {BCD} \right)\\C{\rm{D}} \bot B{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABD} \right) \Rightarrow C{\rm{D}} \bot A{\rm{D}}\)
Vậy tam giác \(ACD\) vuông tại \(D\).
Trong Hình 54, hai bìa của cuốn sách gợi nên hình ảnh hai mặt phẳng vuông góc với mặt bàn. Hãy dự đoán xem gáy sách có vuông góc với mặt bàn hay không.

Phương pháp giải:
Quan sát hình ảnh và trả lời câu hỏi.
Lời giải chi tiết:
Gáy sách vuông góc với mặt bàn.
Cho hình chóp \(S.ABC\) có \(SA \bot SB,SB \bot SC,SC \bot SA\). Chứng minh rằng:
a) \(\left( {SAB} \right) \bot \left( {SBC} \right)\);
b) \(\left( {SBC} \right) \bot \left( {SCA} \right)\);
c) \(\left( {SCA} \right) \bot \left( {SAB} \right)\).
Phương pháp giải:
Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
Lời giải chi tiết:

a) Ta có:
\(\left. \begin{array}{l}\left. \begin{array}{l}SA \bot SB\\SA \bot SC\end{array} \right\} \Rightarrow SA \bot \left( {SBC} \right)\\SA \subset \left( {SAB} \right)\end{array} \right\} \Rightarrow \left( {SAB} \right) \bot \left( {SBC} \right)\)
b) Ta có:
\(\left. \begin{array}{l}\left. \begin{array}{l}SA \bot SB\\SA \bot SC\end{array} \right\} \Rightarrow SA \bot \left( {SBC} \right)\\SA \subset \left( {SCA} \right)\end{array} \right\} \Rightarrow \left( {SCA} \right) \bot \left( {SBC} \right)\)
c) Ta có:
\(\left. \begin{array}{l}\left. \begin{array}{l}SA \bot SB\\SB \bot SC\end{array} \right\} \Rightarrow SB \bot \left( {SCA} \right)\\SB \subset \left( {SAB} \right)\end{array} \right\} \Rightarrow \left( {SAB} \right) \bot \left( {SCA} \right)\)
Mục 3 trong SGK Toán 11 tập 2 - Cánh Diều tập trung vào các kiến thức về đường thẳng và mặt phẳng trong không gian. Đây là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững các định nghĩa, tính chất và phương pháp chứng minh liên quan. Việc giải các bài tập trong mục này sẽ giúp các em củng cố kiến thức và rèn luyện kỹ năng giải toán không gian.
Bài tập này yêu cầu học sinh xác định vị trí tương đối (đồng phẳng, cắt nhau, song song, chéo nhau) của hai đường thẳng trong không gian. Để giải bài tập này, học sinh cần nắm vững các định nghĩa và tính chất của các vị trí tương đối này. Ngoài ra, học sinh cũng cần biết cách sử dụng các công cụ như vectơ chỉ phương và vectơ hướng để xác định vị trí tương đối của hai đường thẳng.
Bài tập này yêu cầu học sinh tính góc giữa hai đường thẳng trong không gian. Để giải bài tập này, học sinh cần nắm vững công thức tính góc giữa hai đường thẳng sử dụng tích vô hướng của hai vectơ chỉ phương. Ngoài ra, học sinh cũng cần biết cách tìm vectơ pháp tuyến của mặt phẳng chứa hai đường thẳng để tính góc giữa chúng.
Công thức: cos(θ) = |(a.b)| / (||a|| * ||b||), trong đó a và b là vectơ chỉ phương của hai đường thẳng, θ là góc giữa hai đường thẳng.
Bài tập này yêu cầu học sinh tính khoảng cách từ một điểm đến một đường thẳng trong không gian. Để giải bài tập này, học sinh cần nắm vững công thức tính khoảng cách từ một điểm đến một đường thẳng sử dụng tích có hướng của hai vectơ. Ngoài ra, học sinh cũng cần biết cách tìm hình chiếu của điểm lên đường thẳng để tính khoảng cách.
Công thức: d = |[a x (M - A)]| / ||a||, trong đó a là vectơ chỉ phương của đường thẳng, M là điểm cần tính khoảng cách, A là một điểm bất kỳ trên đường thẳng.
(Phần này sẽ trình bày lời giải chi tiết cho từng bài tập trong mục 3 trang 97, 98, 99 SGK Toán 11 tập 2 - Cánh Diều. Mỗi bài tập sẽ được giải thích rõ ràng, từng bước, kèm theo các hình vẽ minh họa nếu cần thiết.)
Các kiến thức về đường thẳng và mặt phẳng trong không gian có ứng dụng rộng rãi trong thực tế, đặc biệt trong các lĩnh vực như kiến trúc, xây dựng, hàng không, và vũ trụ. Việc nắm vững các kiến thức này sẽ giúp các em hiểu sâu hơn về thế giới xung quanh và có thể áp dụng vào giải quyết các vấn đề thực tế.
Để củng cố kiến thức, các em có thể tự giải thêm các bài tập sau:
Hy vọng rằng với lời giải chi tiết và dễ hiểu này, các em sẽ nắm vững kiến thức về đường thẳng và mặt phẳng trong không gian và đạt kết quả tốt nhất trong học tập. Hãy tiếp tục luyện tập và khám phá thêm nhiều kiến thức thú vị khác tại giaitoan.edu.vn!