Bài 6 trang 94 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Cánh diều, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này đòi hỏi học sinh phải nắm vững các công thức đạo hàm cơ bản và kỹ năng giải quyết bài toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 6 trang 94 SGK Toán 11 tập 2, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\). Gọi \(\alpha \) là số đo của góc nhị diện \(\left[ {A,BC,S} \right]\).
Đề bài
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\). Gọi \(\alpha \) là số đo của góc nhị diện \(\left[ {A,BC,S} \right]\). Chứng minh rằng tỉ số diện tích của hai tam giác \(ABC\) và \(SBC\) bằng \(\cos \alpha \).
Phương pháp giải - Xem chi tiết
‒ Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)
Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).
Bước 2: Tìm mặt phẳng \(\left( R \right) \supset c\).
Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).
Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).
Lời giải chi tiết
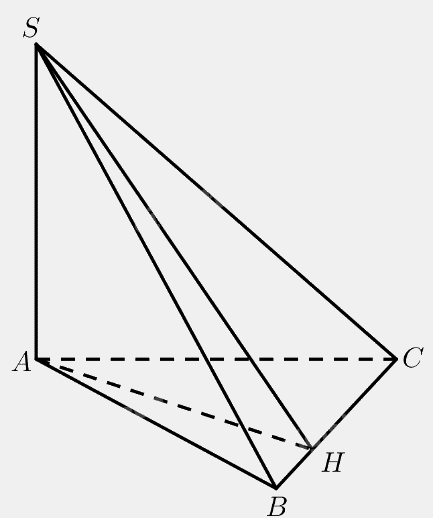
Kẻ \(AH \bot BC\left( {H \in BC} \right)\)
\(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\)
\( \Rightarrow BC \bot \left( {SAH} \right) \Rightarrow BC \bot SH\)
Vậy \(\widehat {SHA}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,BC,S} \right]\)
\( \Rightarrow \widehat {SHA} = \alpha \)
\(\begin{array}{l}{S_{\Delta ABC}} = \frac{1}{2}BC.AH,{S_{\Delta SBC}} = \frac{1}{2}BC.SH\\ \Rightarrow \frac{{{S_{\Delta ABC}}}}{{{S_{\Delta SBC}}}} = \frac{{\frac{1}{2}BC.AH}}{{\frac{1}{2}BC.SH}} = \frac{{AH}}{{SH}} = \cos \widehat {SHA} = \cos \alpha \end{array}\)
Bài 6 trang 94 SGK Toán 11 tập 2 - Cánh diều là một bài tập quan trọng trong chương trình học Toán 11, yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến tốc độ thay đổi của hàm số.
Bài tập yêu cầu học sinh tính đạo hàm của hàm số tại một điểm cho trước, hoặc tìm điểm mà tại đó đạo hàm bằng một giá trị cụ thể. Để giải quyết bài tập này, học sinh cần nắm vững các quy tắc tính đạo hàm của các hàm số cơ bản, như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit, và các quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số.
Ví dụ: Cho hàm số f(x) = x2 + 2x + 1. Tính f'(2).
Giải:
Vậy, f'(2) = 6.
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, học sinh có thể tham khảo các bài tập tương tự trong SGK Toán 11 tập 2 - Cánh diều, hoặc trên các trang web học toán online uy tín.
Đạo hàm là một khái niệm quan trọng trong Toán học, có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như vật lý, kinh tế, kỹ thuật, và khoa học máy tính. Việc nắm vững kiến thức về đạo hàm giúp học sinh hiểu rõ hơn về các hiện tượng tự nhiên và xã hội, và có khả năng giải quyết các bài toán thực tế một cách hiệu quả.
Bài 6 trang 94 SGK Toán 11 tập 2 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và rèn luyện kỹ năng giải bài tập. Hy vọng rằng, với lời giải chi tiết và hướng dẫn cụ thể tại giaitoan.edu.vn, học sinh sẽ tự tin hơn trong việc học tập và đạt kết quả tốt trong môn Toán.