Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong sách giáo khoa Toán 11 tập 1 - Cánh Diều.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt trong môn Toán.
Xét hàm số (fleft( x right) = 2x.) a) Xét dãy số (left( {{x_n}} right),) với ({x_n} = 1 + frac{1}{n}.) Hoàn thành bảng giá trị (fleft( {{x_n}} right)) tương ứng.
Xét hàm số \(f\left( x \right) = 2x.\)
a) Xét dãy số \(\left( {{x_n}} \right),\) với \({x_n} = 1 + \frac{1}{n}.\) Hoàn thành bảng giá trị \(f\left( {{x_n}} \right)\) tương ứng.
Các giá trị tương ứng của hàm số \(f\left( {{x_1}} \right),f\left( {{x_2}} \right),...,f\left( {{x_n}} \right),...\) lập thành một dãy số mà ta kí hiệu là \(\left( {f\left( {{x_n}} \right)} \right).\) Tìm \(\lim f\left( {{x_n}} \right).\)
b) Chứng minh rằng với dãy số bất kì \(\left( {{x_n}} \right),{x_n} \to 1\) ta luôn có \(f\left( {{x_n}} \right) \to 2.\)
Phương pháp giải:
Sử dụng định lí về giới hạn hữu hạn kết hợp với một số giới hạn cơ bản.
Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to + \infty } {v_n} = b\) thì
\(\mathop {\lim }\limits_{n \to + \infty } ({u_n} \pm {v_n}) = a \pm b\)
\(\mathop {\lim }\limits_{n \to + \infty } ({u_n}.{v_n}) = a.b\)
\(\mathop {\lim }\limits_{n \to + \infty } (\frac{{{u_n}}}{{{v_n}}}) = \frac{a}{b}\left( {b \ne 0} \right)\)
Lời giải chi tiết:
a,
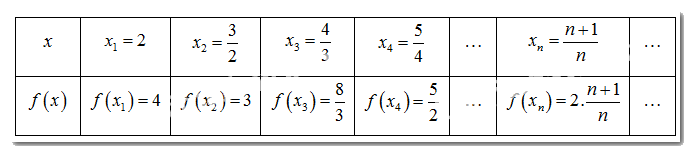
\(\lim f\left( {{x_n}} \right) = \lim \left( {2.\frac{{n + 1}}{n}} \right) = \lim 2.\lim \left( {1 + \frac{1}{n}} \right) = 2.\left( {1 + 0} \right) = 2\)
b) Lấy dãy số bất kì \(\left( {{x_n}} \right),{x_n} \to 1\) ta có \(f\left( {{x_n}} \right) = 2{x_n}.\)
\(\lim f\left( {{x_n}} \right) = \lim \left( {2{x_n}} \right) = \lim 2.\lim {x_n} = 2.1 = 2\)
Sử dụng định nghĩa, chứng minh rằng \(\mathop {\lim }\limits_{x \to 2} {x^2} = 4.\)
Phương pháp giải:
Sử dụng định nghĩa giới hạn hữu hạn của hàm số tại một điểm
Cho khoảng K chứa điểm \({x_0}\)và hàm số \(f(x)\)xác định trên K hoặc trên \(K\backslash \left\{ {{x_0}} \right\}\). Hàm số \(f(x)\)có giới hạn là số L khi \(x\) dần tới \({x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\)bất kì, \({x_n} \in K\backslash \left\{ {{x_0}} \right\}\) và \({x_n} \to {x_0}\), ta có\(f({x_n}) \to L\)
Lời giải chi tiết:
Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thỏa mãn \(\lim {x_n} = 2.\)
Ta có \(\lim x_n^2 = {2^2} = 4\)
Vậy \(\mathop {\lim }\limits_{x \to 2} {x^2} = 4.\)
Cho hai hàm số \(f\left( x \right) = {x^2} - 1,g\left( x \right) = x + 1.\)
a) Tính \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\) và \(\mathop {\lim }\limits_{x \to 1} g\left( x \right).\)
b) Tính \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right]\)và so sánh \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right).\)
c) Tính \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) - g\left( x \right)} \right]\)và so sánh \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) - \mathop {\lim }\limits_{x \to 1} g\left( x \right).\)
d) Tính \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right).g\left( x \right)} \right]\)và so sánh \(\mathop {\lim }\limits_{x \to 1} f\left( x \right).\mathop {\lim }\limits_{x \to 1} g\left( x \right).\)
e) Tính \(\mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right)}}{{g\left( x \right)}}\)và so sánh \(\frac{{\mathop {\lim }\limits_{x \to 1} f\left( x \right)}}{{\mathop {\lim }\limits_{x \to 1} g\left( x \right)}}.\)
Phương pháp giải:
\(\mathop {\lim }\limits_{x \to {x_0}} x = {x_0};\mathop {\lim }\limits_{x \to {x_0}} c = c\)
Lời giải chi tiết:
a) \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} - 1} \right) = \mathop {\lim }\limits_{x \to 1} {x^2} - \mathop {\lim }\limits_{x \to 1} 1 = {1^2} - 1 = 0\)
\(\mathop {\lim }\limits_{x \to 1} g\left( x \right) = \mathop {\lim }\limits_{x \to 1} \left( {x + 1} \right) = \mathop {\lim }\limits_{x \to 1} x + \mathop {\lim }\limits_{x \to 1} 1 = 1 + 1 = 2\)
b) \(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} + x} \right) = {1^2} + 1 = 2\\\mathop {\lim }\limits_{x \to 1} f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right) = 0 + 2 = 2\\ \Rightarrow \mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right).\end{array}\)
c) \(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) - g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} - x - 2} \right) = {1^2} - 1 - 2 = - 2\\\mathop {\lim }\limits_{x \to 1} f\left( x \right) - \mathop {\lim }\limits_{x \to 1} g\left( x \right) = 0 - 2 = - 2\\ \Rightarrow \mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) - g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} f\left( x \right) - \mathop {\lim }\limits_{x \to 1} g\left( x \right).\end{array}\)
d) \(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right).g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} \left[ {\left( {{x^2} - 1} \right)\left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to 1} \left( {{x^3} + {x^2} - x - 1} \right) = {1^3} + {1^2} - 1 - 1 = 0\\\mathop {\lim }\limits_{x \to 1} f\left( x \right).\mathop {\lim }\limits_{x \to 1} g\left( x \right) = 0.2 = 0\\ \Rightarrow \mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right).g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} f\left( x \right).\mathop {\lim }\limits_{x \to 1} g\left( x \right).\end{array}\)
e) \(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right)}}{{g\left( x \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x + 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {x - 1} \right)\left( {x + 1} \right)}}{{x + 1}} = \mathop {\lim }\limits_{x \to 1} \left( {x - 1} \right) = 1 - 1 = 0\\\frac{{\mathop {\lim }\limits_{x \to 1} f\left( x \right)}}{{\mathop {\lim }\limits_{x \to 1} g\left( x \right)}} = \frac{0}{2} = 0\\ \Rightarrow \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{\mathop {\lim }\limits_{x \to 1} f\left( x \right)}}{{\mathop {\lim }\limits_{x \to 1} g\left( x \right)}}.\end{array}\)
Tính:
a) \(\mathop {\lim }\limits_{x \to 2} \left[ {\left( {x + 1} \right)\left( {{x^2} + 2x} \right)} \right];\)
b) \(\mathop {\lim }\limits_{x \to 2} \sqrt {{x^2} + x + 3} .\)
Phương pháp giải:
Sử dụng định lí về phép toán trên giới hạn hữu hạn của hàm số
Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\)và \(\mathop {\lim }\limits_{x \to {x_0}} g(x) = M\)\(\left( {L,M \in \mathbb{R}} \right)\)thì
\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x) \pm g(x)} \right] = L \pm M\)
\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x).g(x)} \right] = L.M\)
\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {\frac{{f(x)}}{{g(x)}}} \right] = \frac{L}{M}\left( {M \ne 0} \right)\)
Nếu \(f(x) \ge 0\)với mọi \(x \in \left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}\) và \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\) thì \(L \ge 0\)và \(\mathop {\lim }\limits_{x \to {x_0}} \sqrt {f(x)} = \sqrt L \).
Lời giải chi tiết:
a) \(\mathop {\lim }\limits_{x \to 2} \left[ {\left( {x + 1} \right)\left( {{x^2} + 2x} \right)} \right] = \mathop {\lim }\limits_{x \to 2} \left( {x + 1} \right).\mathop {\lim }\limits_{x \to 2} \left( {{x^2} + 2x} \right) = \left( {2 + 1} \right).\left( {{2^2} + 2.2} \right) = 24\)
b) \(\mathop {\lim }\limits_{x \to 2} \sqrt {{x^2} + x + 3} = \sqrt {\mathop {\lim }\limits_{x \to 2} \left( {{x^2} + x + 3} \right)} = \sqrt {\mathop {\lim }\limits_{x \to 2} {x^2} + \mathop {\lim }\limits_{x \to 2} x + \mathop {\lim }\limits_{x \to 2} 3} = \sqrt {{2^2} + 2 + 3} = 3\)
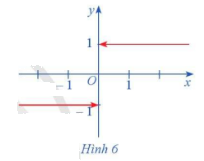
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l} - 1,\,\,x < 0\\0,\,\,x = 0\\1,\,\,x > 0\end{array} \right.\)
Hàm số \(f\left( x \right)\) có đồ thị ở Hình 6.

a) Xét dãy số \(\left( {{u_n}} \right)\) sao cho \({u_n} < 0\) và \(\lim {u_n} = 0.\) Xác định \(f\left( {{u_n}} \right)\) và tìm \(\lim f\left( {{u_n}} \right).\)
b) Xét dãy số \(\left( {{v_n}} \right)\) sao cho \({v_n} > 0\) và \(\lim {v_n} = 0.\) Xác định \(f\left( {{v_n}} \right)\) và tìm \(\lim f\left( {{v_n}} \right).\)
Phương pháp giải:
Quan sát đồ thị hình 6 để trả lời câu hỏi.
Lời giải chi tiết:
a) Xét dãy số \(\left( {{u_n}} \right)\) sao cho \({u_n} < 0\) và \(\lim {u_n} = 0.\) Khi đó \(f\left( {{u_n}} \right) = - 1\) và \(\lim f\left( {{u_n}} \right) = - 1.\)
b) Xét dãy số \(\left( {{v_n}} \right)\) sao cho \({v_n} > 0\) và \(\lim {v_n} = 0.\) Khi đó \(f\left( {{v_n}} \right) = 1\) và \(\lim f\left( {{v_n}} \right) = 1.\)
Tính \(\mathop {\lim }\limits_{x \to - {4^ + }} \left( {\sqrt {x + 4} + x} \right)\)
Phương pháp giải:
Sử dụng định nghĩa giới hạn một phía.
- Cho hàm số \(y = f(x)\)xác định trên khoảng \(\left( {a;{x_0}} \right)\). Số L được gọi là giới hạn bên trái của hàm số \(y = f(x)\)khi \(x \to {x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\)bất kì thỏa mãn \(a < {x_n} < {x_0}\) và \({x_n} \to {x_0}\)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = L\).
- Cho hàm số \(y = f(x)\)xác định trên khoảng \(\left( {{x_0};b} \right)\). Số L là giới hạn bên của hàm số \(y = f(x)\) khi \(x \to {x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\)bất kì thỏa mãn \({x_0} < {x_n} < b\) và \({x_n} \to {x_0}\)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = L\).
Lời giải chi tiết:
Với dãy số \(\left( {{x_n}} \right)\) bất kì \({x_n} > - 4\) và \({x_n} \to - 4,\) ta có:
\(\begin{array}{c}\mathop {\lim }\limits_{{x_n} \to - {4^ + }} \left( {\sqrt {{x_n} + 4} + {x_n}} \right) = \mathop {\lim }\limits_{{x_n} \to - {4^ + }} \sqrt {{x_n} + 4} + \mathop {\lim }\limits_{{x_n} \to - {4^ + }} {x_n} = \sqrt {\mathop {\lim }\limits_{{x_n} \to - {4^ + }} \left( {{x_n} + 4} \right)} + \left( { - 4} \right)\\ = \sqrt {\mathop {\lim }\limits_{{x_n} \to - {4^ + }} {x_n} + 4} - 4 = \sqrt { - 4 + 4} - 4 = - 4\end{array}\)
Vậy \(\mathop {\lim }\limits_{x \to - {4^ + }} \left( {\sqrt {x + 4} + x} \right) = - 4\)
Mục 1 của SGK Toán 11 tập 1 - Cánh Diều tập trung vào các kiến thức cơ bản về giới hạn của hàm số. Đây là một khái niệm quan trọng, nền tảng cho việc học tập các kiến thức nâng cao hơn trong chương trình Toán học. Việc nắm vững các định nghĩa, tính chất và phương pháp tính giới hạn là vô cùng cần thiết.
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 1, trang 66, 67, 68, 69 SGK Toán 11 tập 1 - Cánh Diều:
a) lim (x→2) (x^2 + 3x - 1)
Lời giải: Thay x = 2 vào biểu thức, ta được: 2^2 + 3*2 - 1 = 4 + 6 - 1 = 9. Vậy lim (x→2) (x^2 + 3x - 1) = 9.
b) lim (x→-1) (x^3 - 2x + 5)
Lời giải: Thay x = -1 vào biểu thức, ta được: (-1)^3 - 2*(-1) + 5 = -1 + 2 + 5 = 6. Vậy lim (x→-1) (x^3 - 2x + 5) = 6.
a) lim (x→3) (2x + 1)/(x - 1)
Lời giải: Thay x = 3 vào biểu thức, ta được: (2*3 + 1)/(3 - 1) = 7/2. Vậy lim (x→3) (2x + 1)/(x - 1) = 7/2.
b) lim (x→0) (x^2 + 1)/(x + 2)
Lời giải: Thay x = 0 vào biểu thức, ta được: (0^2 + 1)/(0 + 2) = 1/2. Vậy lim (x→0) (x^2 + 1)/(x + 2) = 1/2.
Để giải các bài tập về giới hạn một cách hiệu quả, các em cần nắm vững các phương pháp sau:
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trên đây, các em học sinh sẽ hiểu rõ hơn về Mục 1 SGK Toán 11 tập 1 - Cánh Diều và tự tin giải quyết các bài tập liên quan. Chúc các em học tập tốt!