Bài 5 trang 100 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 tập 1, Cánh diều. Bài tập này tập trung vào việc rèn luyện kỹ năng về đạo hàm của hàm số, đặc biệt là đạo hàm của tổng, hiệu, tích, thương của các hàm số.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và phương pháp giải bài tập.
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn và (AB = 2CD).Gọi M, N lần lượt là trung điểm của các cạnh SA và SB. Chứng minh rằng đường thẳng NC song song với đường thẳng MD.
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn và \(AB = 2CD\).Gọi M, N lần lượt là trung điểm của các cạnh SA và SB. Chứng minh rằng đường thẳng NC song song với đường thẳng MD.
Phương pháp giải - Xem chi tiết
Hình bình hành là hình có các cặp cạnh đối song song và bằng nhau.
Đường trung bình của tam giác là đường đi qua trung điểm 2 cạnh, đường trung bình song song với đáy và bằng nửa cạnh đáy.
Lời giải chi tiết
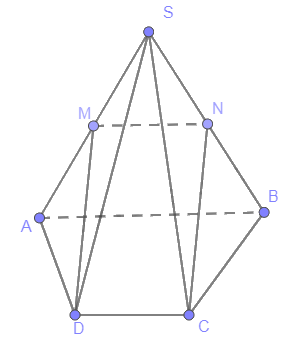
Ta có:MN là đường trung bình của tam giác SAB \(\Rightarrow MN//AB, MN= \frac{1}{2}AB \)
Mà \(\ CD//AB, CD= \frac{1}{2}AB \)
Suy ra: MN//CD, MN = CD.
Từ (1) và (2) suy ra MNCD là hình bình hành
Vậy NC // MD.
Bài 5 yêu cầu chúng ta tính đạo hàm của các hàm số đã cho. Để giải bài này, chúng ta cần nắm vững các quy tắc tính đạo hàm cơ bản như đạo hàm của tổng, hiệu, tích, thương và đạo hàm của các hàm số sơ cấp.
Để tính đạo hàm của hàm số này, ta áp dụng quy tắc đạo hàm của tổng: (u + v)' = u' + v'.
y' = (x4)' + (5x2)' + (3)'
Sử dụng quy tắc đạo hàm của lũy thừa: (xn)' = nxn-1, ta có:
y' = 4x3 + 10x + 0 = 4x3 + 10x
Tương tự, ta áp dụng quy tắc đạo hàm của tổng và hiệu, đồng thời sử dụng quy tắc đạo hàm của thương: (u/v)' = (u'v - uv')/v2.
y' = (3x)' - (2/x)' + (1)'
y' = 3 - 2(-1/x2) + 0 = 3 + 2/x2
Áp dụng quy tắc đạo hàm của tích: (uv)' = u'v + uv'.
y' = (x2 + 1)'(x - 2) + (x2 + 1)(x - 2)'
y' = (2x)(x - 2) + (x2 + 1)(1) = 2x2 - 4x + x2 + 1 = 3x2 - 4x + 1
Áp dụng quy tắc đạo hàm của thương: (u/v)' = (u'v - uv')/v2.
y' = (x2)'(x + 1) - (x2)(x + 1)' / (x + 1)2
y' = (2x)(x + 1) - (x2)(1) / (x + 1)2 = (2x2 + 2x - x2) / (x + 1)2 = (x2 + 2x) / (x + 1)2
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Bài 5 trang 100 SGK Toán 11 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Bằng cách nắm vững các quy tắc đạo hàm và thực hành nhiều bài tập, học sinh có thể tự tin giải quyết các bài toán liên quan đến đạo hàm.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về bài tập và đạt kết quả tốt trong học tập.