Chào mừng bạn đến với bài học về Lý thuyết Phép tính lũy thừa với số mũ thực dành cho học sinh lớp 11 chương trình Cánh diều. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và quan trọng nhất về chủ đề này.
Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất, các dạng bài tập thường gặp và phương pháp giải chúng. Mục tiêu là giúp bạn hiểu sâu sắc và vận dụng linh hoạt kiến thức vào giải quyết các bài toán thực tế.
1. Phép tính lũy thừa với số mũ nguyên
1. Phép tính lũy thừa với số mũ nguyên
Cho số thực a khác 0 và số nguyên dương n. Ta đặt \({a^{ - n}} = \frac{1}{{{a^n}}}\).
Chú ý:
- \({0^0}\) và \({0^{ - n}}\) (n nguyên dương) không có nghĩa.
- Lũy thừa với số mũ nguyên có các tính chất tương tự của lũy thừa với số mũ nguyên dương.
2. Căn bậc n
a) Định nghĩa
Cho số thực a và số nguyên dương n (n \( \ge \) 2). Số b được gọi là căn bậc n của số a nếu \({b^n} = a\).
Nhận xét:
- Với n lẻ và a \( \in \mathbb{R}\): Có duy nhất một căn bậc n của a, kí hiệu là \(\sqrt[n]{a}\).
- Với n chẵn, ta xét ba trường hợp sau:
+) a < 0: Không tồn tại căn bậc n của a.
+) a = 0: Có một căn bậc n của a là số 0.
+) a > 0: Có hai căn bậc n của a là hai số đối nhau, giá trị dương kí hiệu là \(\sqrt[n]{a}\), còn giá trị âm kí hiệu là \( - \sqrt[n]{a}\).
b) Tính chất
(Ở mỗi công thức trên, ta giả sử các biểu thức xuất hiện trong đó là có nghĩa).
3. Phép tính lũy thừa với số mũ hữu tỉ
Cho số thực a dương và số hữu tỉ \(r = \frac{m}{n}\), trong đó \(m \in \mathbb{Z},n \in \mathbb{N},n \ge 2\). Lũy thừa của a với số mũ r xác định bởi: \({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\).
Nhận xét:
4. Phép tính lũy thừa với số mũ thực
a) Định nghĩa
Cho a là số thực dương, \(\alpha \) là số vô tỉ, \(\left( {{r_n}} \right)\) là dãy số hữu tỉ và \(\lim {r_n} = \alpha \). Giới hạn của dãy số \(\left( {{a^{{r_n}}}} \right)\) gọi là lũy thừa của a với số mũ \(\alpha \), kí hiệu \({a^\alpha }\), \({a^\alpha } = \lim {a^{{r_n}}}\).
b) Tính chất
- Cho a, b là những số thực dương; \(\alpha ,\beta \) là những số thực tùy ý. Khi đó, ta có:
\({a^\alpha }.{a^\beta } = {a^{\alpha + \beta }}\); \({\left( {ab} \right)^\alpha } = {a^\alpha }.{b^\alpha }\); \({\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{{{b^\alpha }}}\); \(\frac{{{a^\alpha }}}{{{a^\beta }}} = {a^{\alpha - \beta }}\); \({\left( {{a^\alpha }} \right)^\beta } = {a^{\alpha \beta }}\).
- Nếu a > 1 thì \({a^\alpha } > {a^\beta } \Leftrightarrow \alpha > \beta \).
Nếu 0 < a < 1 thì \({a^\alpha } > {a^\beta } \Leftrightarrow \alpha < \beta \).
- Cho 0 < a < b, \(\alpha \) là một số thực. Ta có:
\({a^\alpha } < {b^\alpha } \Leftrightarrow \alpha > 0\); \({a^\alpha } > {b^\alpha } \Leftrightarrow \alpha < 0\).
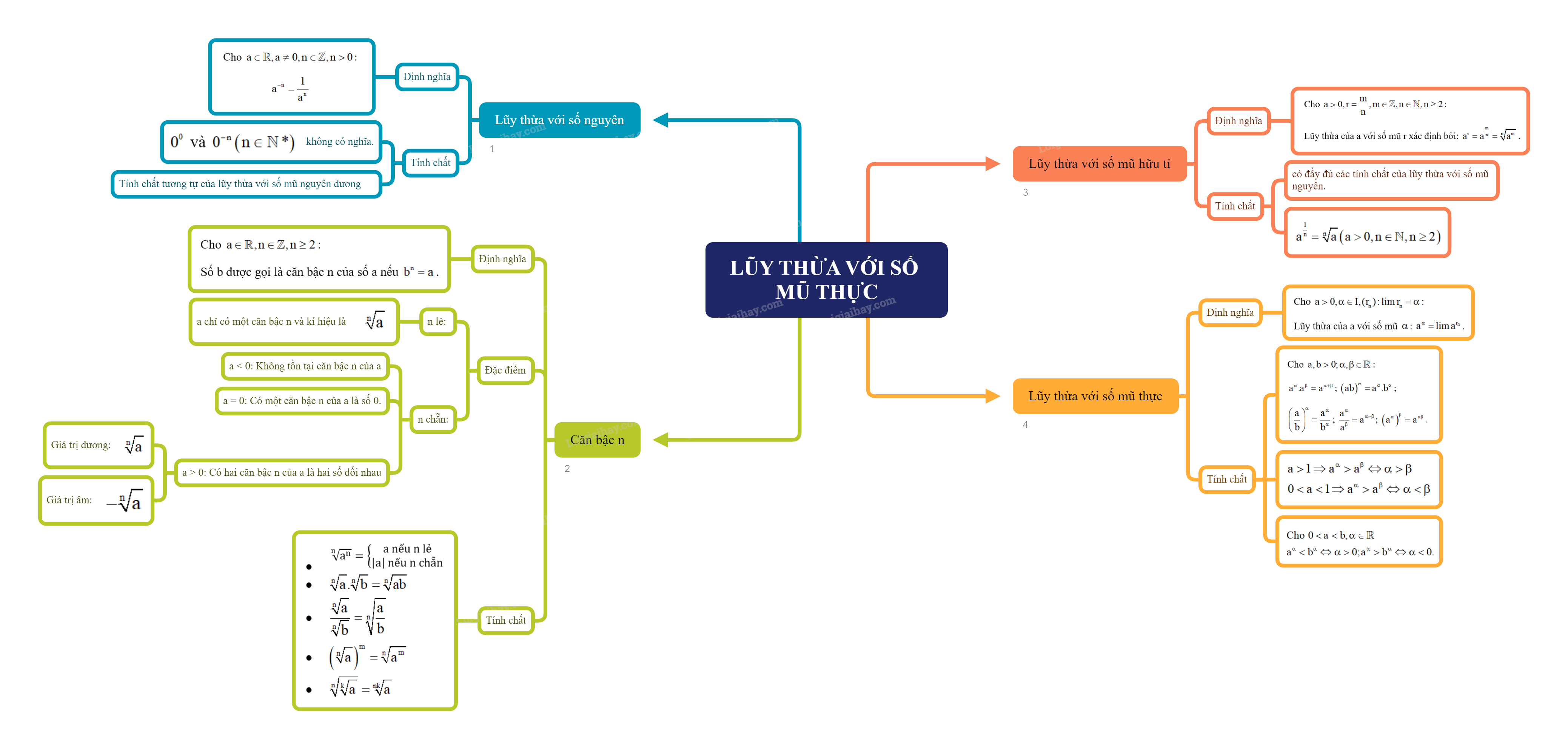
Phép tính lũy thừa với số mũ thực là một phần quan trọng trong chương trình Toán 11, đặc biệt là trong chương trình Cánh diều. Nó mở rộng khái niệm lũy thừa từ số mũ nguyên sang số mũ thực, cho phép chúng ta biểu diễn và tính toán các biểu thức phức tạp hơn.
Với a > 0 và α là một số thực bất kỳ, lũy thừa của a với số mũ α, ký hiệu là aα, là một số thực duy nhất được xác định bởi các tính chất sau:
Trong đó, e là cơ số của logarit tự nhiên (e ≈ 2.71828) và ln(a) là logarit tự nhiên của a.
Các tính chất của lũy thừa với số mũ thực tương tự như lũy thừa với số mũ nguyên, nhưng cần lưu ý một số điểm sau:
Lưu ý: Các tính chất trên chỉ đúng khi a > 0 và b > 0.
Các bài tập về lũy thừa với số mũ thực thường gặp các dạng sau:
Để giải các bài tập về lũy thừa với số mũ thực, bạn có thể áp dụng các phương pháp sau:
Ví dụ 1: Tính giá trị của 21.5
Giải: 21.5 = 23/2 = √(23) = √8 = 2√2
Ví dụ 2: Rút gọn biểu thức (32 * 3-1) / 30.5
Giải: (32 * 3-1) / 30.5 = 32-1-0.5 = 30.5 = √3
Để nắm vững kiến thức về lũy thừa với số mũ thực, bạn nên luyện tập thường xuyên với các bài tập khác nhau. Hãy tìm kiếm các bài tập trong sách giáo khoa, sách bài tập hoặc trên các trang web học toán online như giaitoan.edu.vn.
Hy vọng bài học này đã cung cấp cho bạn những kiến thức hữu ích về Lý thuyết Phép tính lũy thừa với số mũ thực - Toán 11 Cánh diều. Chúc bạn học tập tốt!