Cấp số cộng là một trong những kiến thức cơ bản và quan trọng trong chương trình Toán 11, đặc biệt theo SGK Cánh Diều. Việc nắm vững lý thuyết này không chỉ giúp bạn giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng cho các kiến thức nâng cao hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu về lý thuyết Cấp số cộng, kèm theo các ví dụ minh họa và bài tập thực hành để bạn có thể tự tin chinh phục môn Toán.
1. Định nghĩa
1. Định nghĩa
Cấp số cộng là một dãy số ,trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d. Tức là:
\({u_n} = {u_{n - 1}} + d,n \ge 2\)
Số d được gọi là công sai của cấp số cộng.
* Nhận xét: Nếu \(\left( {{u_n}} \right)\) là cấp số cộng thì kể từ số hạng thứ 2, mỗi số hạng (trừ số hạng cuối đối với cấp số cộng hữu hạn) đều là trung bình cộng của 2 sô hạng đứng kề nó trong dãy, tức là:
\({u_k} = \frac{{{u_{k - 1}} + {u_{k + 1}}}}{2}\left( {k \ge 2} \right)\)
2. Số hạng tổng quát
Nếu cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu là \({u_1}\) và công sai d thì số hạng tổng quát \({u_n}\)của nó được xác định theo công thức\({u_n} = {u_1} + (n - 1)d,n \ge 2.\)
3. Tổng n số hạng đầu của một cấp số cộng
Cho cấp số cộng \(\left( {{u_n}} \right)\)với công sai d. Đặt \({S_n} = {u_1} + {u_2} + {u_3} + ... + {u_n}\). Khi đó
\({S_n} = \frac{{n\left( {{u_1} + {u_n}} \right)}}{2} = \frac{n}{2}\left[ {2{u_1} + \left( {n - 1} \right)d} \right]\)
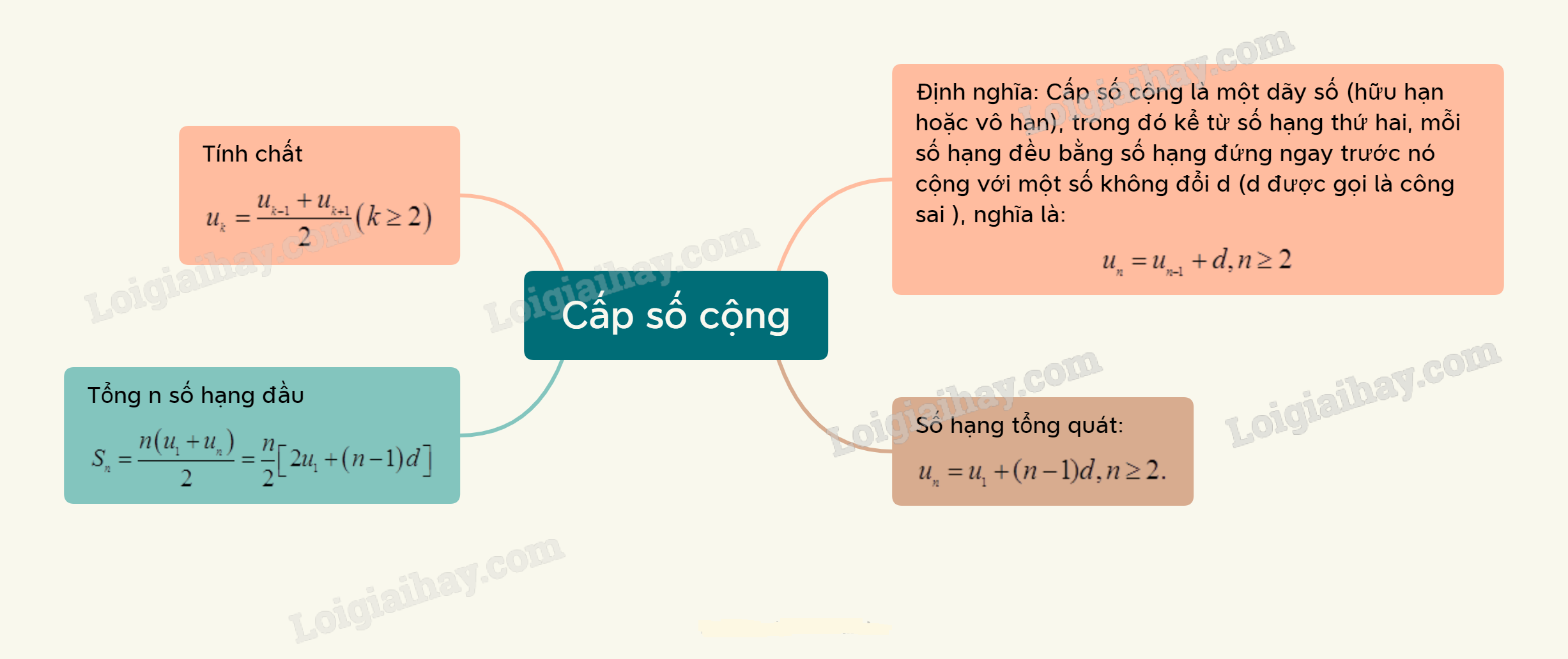
Cấp số cộng là một dãy số mà mỗi số hạng sau được tạo thành bằng cách cộng một số không đổi vào số hạng đứng trước nó. Số không đổi này được gọi là công sai của cấp số cộng.
Một dãy số (un) được gọi là cấp số cộng nếu có một số công sai d sao cho:
Số d được gọi là công sai của cấp số cộng.
Số hạng tổng quát của cấp số cộng (un) được xác định bởi công thức:
un = u1 + (n - 1)d
Trong đó:
Một số tính chất quan trọng của cấp số cộng:
Tổng của n số hạng đầu tiên của cấp số cộng (Sn) được tính theo công thức:
Sn = (n/2)(u1 + un) = (n/2)[2u1 + (n - 1)d]
Các bài tập về cấp số cộng thường gặp các dạng sau:
Ví dụ 1: Cho cấp số cộng có số hạng đầu u1 = 2 và công sai d = 3. Tìm số hạng thứ 5 của cấp số cộng.
Giải:
u5 = u1 + (5 - 1)d = 2 + 4 * 3 = 14
Ví dụ 2: Cho cấp số cộng có số hạng đầu u1 = 1 và tổng của 10 số hạng đầu tiên là S10 = 55. Tìm công sai d.
Giải:
S10 = (10/2)[2u1 + (10 - 1)d] = 5[2 + 9d] = 55
=> 2 + 9d = 11
=> 9d = 9
=> d = 1
Để nắm vững kiến thức về cấp số cộng, bạn nên luyện tập thường xuyên các bài tập khác nhau. Tại giaitoan.edu.vn, chúng tôi cung cấp một hệ thống bài tập đa dạng, từ cơ bản đến nâng cao, kèm theo đáp án chi tiết để bạn có thể tự kiểm tra và đánh giá kết quả học tập của mình.
Lý thuyết Cấp số cộng là một phần quan trọng trong chương trình Toán 11. Việc hiểu rõ các định nghĩa, công thức và tính chất của cấp số cộng sẽ giúp bạn giải quyết các bài toán một cách hiệu quả và tự tin. Hãy truy cập giaitoan.edu.vn để học tập và luyện tập ngay hôm nay!