Bài 4 trang 65 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Cánh Diều, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến phép biến hóa lượng giác. Bài tập này đòi hỏi học sinh nắm vững kiến thức về công thức lượng giác cơ bản và khả năng vận dụng linh hoạt vào giải quyết vấn đề.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn hiểu rõ phương pháp giải và tự tin làm bài tập.
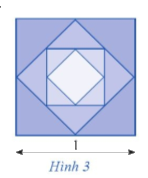
Từ hình vuông có độ dài cạnh bằng 1, người ta nối các trung điểm của cạnh hình vuông để tạo ra hình vuông mới như Hình 3. Tiếp tục quá trình này đến vô hạn. a) Tính diện tích Sn của hình vuông được tạo thành ở bước thứ n; b) Tính tổng diện tích của tất cả các hình vuông được tạo thành.
Đề bài
Từ hình vuông có độ dài cạnh bằng 1, người ta nối các trung điểm của cạnh hình vuông để tạo ra hình vuông mới như Hình 3. Tiếp tục quá trình này đến vô hạn.
a) Tính diện tích \({S_n}\) của hình vuông được tạo thành ở bước thứ n;
b) Tính tổng diện tích của tất cả các hình vuông được tạo thành.
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính tổng n số hạng đầu của cấp số nhân \({S_n} = {u_1}.\frac{{1 - {q^n}}}{{1 - q}}\)
Tổng cấp số nhân lùi vô hạn \(S = \frac{{{u_1}}}{{1 - q}}\).
Lời giải chi tiết
a) Diện tích hình vuông ban đầu bằng 1.1 = 1 (đvdt).
Vì người ta nối các trung điểm của cạnh hình vuông để tạo ra hình vuông mới nên diện tích hình vuông mới sẽ bằng một nửa hình vuông trước.
Do đó ta có \({u_1} = {S_1} = 1,q = \frac{1}{2}\).
Vậy \({S_n} = 1.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{1 - \frac{1}{2}}} = {\left( {\frac{1}{2}} \right)^{n - 1}}\).
b) Diện tích mỗi hình vuông trên tạo thành một cấp số nhân lùi vô hạn. Sử dụng công thức tính tổng cấp số nhân lùi vô hạn, ta được:
\(S = \frac{1}{{1 - \frac{1}{2}}} = 2\).
Bài 4 trang 65 SGK Toán 11 tập 1 - Cánh Diều yêu cầu học sinh giải các bài toán liên quan đến việc chứng minh đẳng thức lượng giác và tìm giá trị của biểu thức lượng giác. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các công thức lượng giác cơ bản, các phương pháp chứng minh đẳng thức lượng giác và kỹ năng biến đổi biểu thức.
Bài 4 bao gồm các câu hỏi nhỏ, mỗi câu hỏi yêu cầu học sinh thực hiện một phép biến đổi lượng giác cụ thể. Ví dụ, học sinh có thể được yêu cầu chứng minh một đẳng thức lượng giác bằng cách sử dụng các công thức biến đổi, hoặc tìm giá trị của một biểu thức lượng giác bằng cách thay thế các giá trị lượng giác đã biết.
Để giải bài 4 trang 65 SGK Toán 11 tập 1 - Cánh Diều, học sinh có thể áp dụng các phương pháp sau:
Câu a: (Ví dụ về một câu hỏi trong bài tập và lời giải chi tiết. Thay thế bằng nội dung thực tế của câu a)
Lời giải:
… (Giải thích chi tiết từng bước giải)
Câu b: (Ví dụ về một câu hỏi trong bài tập và lời giải chi tiết. Thay thế bằng nội dung thực tế của câu b)
Lời giải:
… (Giải thích chi tiết từng bước giải)
Ngoài việc giải bài tập trong SGK, học sinh có thể tìm hiểu thêm về các ứng dụng của lượng giác trong thực tế, chẳng hạn như trong lĩnh vực hàng hải, hàng không, xây dựng, đo đạc,…
Để củng cố kiến thức và kỹ năng, học sinh có thể giải thêm các bài tập tương tự trong các sách bài tập, đề thi thử hoặc trên các trang web học toán online.
Bài 4 trang 65 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải các bài toán lượng giác. Bằng cách nắm vững các công thức lượng giác cơ bản, các phương pháp chứng minh đẳng thức lượng giác và kỹ năng biến đổi biểu thức, học sinh có thể tự tin giải quyết bài toán này một cách hiệu quả.
| Công thức lượng giác | Mô tả |
|---|---|
| sin2x + cos2x = 1 | Đẳng thức lượng giác cơ bản |
| tan x = sin x / cos x | Định nghĩa hàm tan |
| cot x = cos x / sin x | Định nghĩa hàm cot |