Bài 3 trang 47 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Cánh Diều, tập trung vào việc giải các bài toán liên quan đến đạo hàm của hàm số. Bài tập này đòi hỏi học sinh nắm vững kiến thức về các quy tắc tính đạo hàm và áp dụng chúng một cách linh hoạt.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 3 trang 47, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Trong các hàm số sau, hàm số nào đồng biến, hàm số nào nghịch biến trên khoảng xác định của hàm số đó? Vì sao?
Đề bài
Lập bảng biến thiên và vẽ đồ thị hàm số:
a) \(y = {4^x}\)
b) \(y = {\log _{\frac{1}{4}}}x\)
d) \(y = {\log _{\frac{{\sqrt {15} }}{4}}}x\)
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức vừa học để làm
Lời giải chi tiết
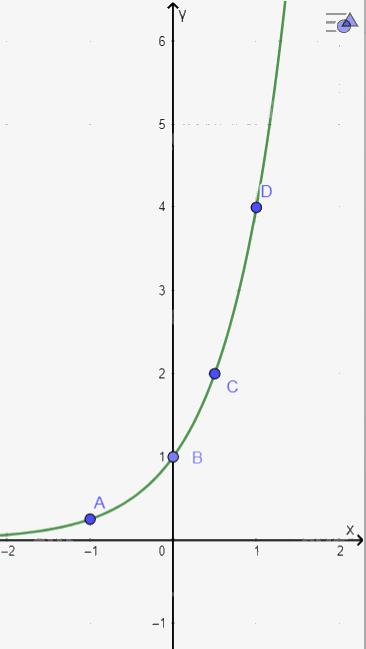
a) Bảng biến thiên\(y = {4^x}\)

Đồ thị hàm số: \(y = {4^x}\)

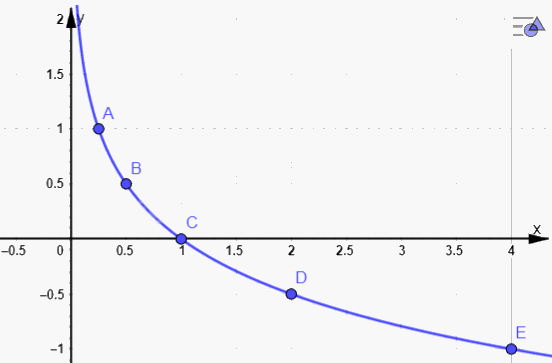
b, Bảng biến thiên:\(y = {\log _{\frac{1}{4}}}x\)

Đồ thị hàm số: \(y = {\log _{\frac{1}{4}}}x\)

Bài 3 trang 47 SGK Toán 11 tập 2 - Cánh Diều yêu cầu học sinh tính đạo hàm của các hàm số cho trước. Để giải bài tập này, chúng ta cần nắm vững các quy tắc đạo hàm cơ bản như đạo hàm của tổng, hiệu, tích, thương và đạo hàm của hàm hợp.
Để tính đạo hàm của hàm số y = x3 - 3x2 + 2x - 5, ta áp dụng quy tắc đạo hàm của tổng và hiệu, kết hợp với quy tắc đạo hàm của lũy thừa:
Vậy, y' = 3x2 - 6x + 2.
Để tính đạo hàm của hàm số y = (x2 + 1)(x - 2), ta áp dụng quy tắc đạo hàm của tích:
(uv)' = u'v + uv'
Trong đó:
Vậy, y' = 2x(x - 2) + (x2 + 1)(1) = 2x2 - 4x + x2 + 1 = 3x2 - 4x + 1.
Để tính đạo hàm của hàm số y = 1/x2, ta có thể viết lại hàm số dưới dạng y = x-2. Sau đó, áp dụng quy tắc đạo hàm của lũy thừa:
y' = -2x-3 = -2/x3.
Để tính đạo hàm của hàm số y = √(x + 1), ta có thể viết lại hàm số dưới dạng y = (x + 1)1/2. Sau đó, áp dụng quy tắc đạo hàm của hàm hợp và đạo hàm của lũy thừa:
y' = (1/2)(x + 1)-1/2 * 1 = 1/(2√(x + 1)).
Bài 3 trang 47 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm. Để giải bài tập này một cách hiệu quả, cần:
Ngoài ra, học sinh nên tham khảo thêm các bài tập tương tự để củng cố kiến thức và kỹ năng. Việc luyện tập thường xuyên sẽ giúp học sinh tự tin hơn khi giải các bài tập về đạo hàm.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về Bài 3 trang 47 SGK Toán 11 tập 2 - Cánh Diều và đạt kết quả tốt trong học tập.
Để hiểu sâu hơn về các khái niệm và phương pháp giải bài tập về đạo hàm, các em có thể tham khảo thêm các tài liệu học tập khác hoặc tìm kiếm sự hỗ trợ từ giáo viên và bạn bè.
Chúc các em học tập tốt!