Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 5 trang 103, 104 SGK Toán 11 tập 2 chương trình Cánh Diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán.
Mục tiêu của chúng tôi là hỗ trợ các em học tập hiệu quả, tiết kiệm thời gian và đạt kết quả cao trong môn Toán.
a) Trong Hình 70, sàn nhà và trần nhà của căn phòng gợi nên hình ảnh hai mặt phẳng song song \(\left( P \right),\left( Q \right)\).
a) Trong Hình 70, sàn nhà và trần nhà của căn phòng gợi nên hình ảnh hai mặt phẳng song song \(\left( P \right),\left( Q \right)\). Chiều cao của căn phòng là 3 m.
Chiều cao đó gợi nên khái niệm gì trong hình học liên quan đến hai mặt phẳng song song \(\left( P \right),\left( Q \right)\)?
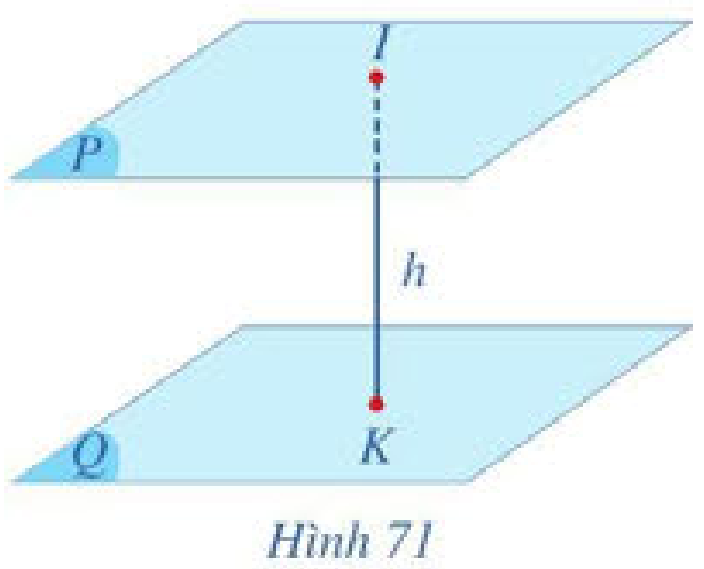
b) Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau. Xét điểm \(I\) tuỳ ý trong mặt phẳng \(\left( P \right)\), lấy \(K\) là hình chiếu của \(I\) trên \(\left( Q \right)\) (Hình 71). Khoảng cách \(IK\) từ điểm \(I\) đến mặt phẳng \(\left( Q \right)\) có phụ thuộc vào vị trí của điểm \(I\) trong mặt phẳng \(\left( P \right)\) hay không? Vì sao?
Phương pháp giải:
Sử dụng tính chất của hai mặt phẳng song song.
Lời giải chi tiết:
a) Khoảng cách đó gợi nên khái niệm khoảng cách giữa hai mặt phẳng song song.
b)
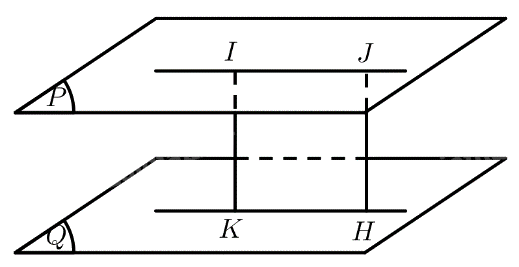
Trên mặt phẳng \(\left( P \right)\) lấy điểm \(J\) khác \(I\).
Kẻ \(JH \bot \left( Q \right)\left( {H \in \left( Q \right)} \right)\)
\( \Rightarrow HKIJ\) là hình chữ nhật \( \Rightarrow IK = JH\)
\( \Rightarrow d\left( {I,\left( Q \right)} \right) = d\left( {J,\left( Q \right)} \right)\)
Vậy khoảng cách \(IK\) từ điểm \(I\) đến mặt phẳng \(\left( Q \right)\) không phụ thuộc vào vị trí của điểm \(I\) trong mặt phẳng \(\left( P \right)\).
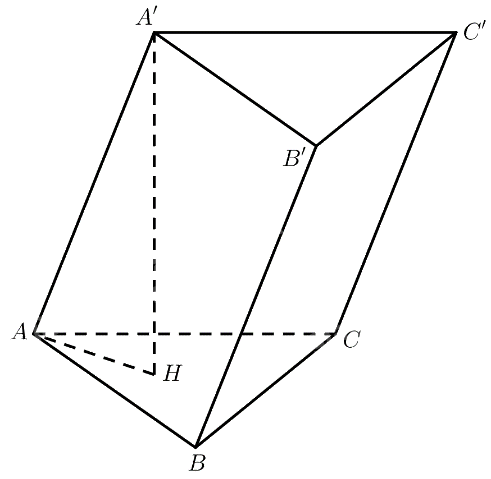
Cho hình lăng trụ \(ABC.A'B'C'\) có cạnh bên bằng \(a\), góc giữa đường thẳng \(AA'\) và mặt phẳng \(\left( {ABC} \right)\) bằng \({60^ \circ }\). Tính khoảng cách giữa hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {A'B'C'} \right)\).
Phương pháp giải:
Cách tính khoảng cách giữa hai mặt phẳng song song: Tính khoảng cách từ một điểm trên mặt phẳng này đến mặt phẳng còn lại.
Lời giải chi tiết:

Gọi \(H\) là hình chiếu vuông góc của \(A'\) lên \(\left( {ABC} \right)\)
\(\begin{array}{l} \Rightarrow A'H \bot \left( {ABC} \right)\\ \Rightarrow \left( {AA',\left( {ABC} \right)} \right) = \left( {AA',AH} \right) = \widehat {A'AH}\end{array}\)
\(\Delta AA'H\) vuông tại \(H \Rightarrow A'H = AA'.\sin \widehat {A'AH} = \frac{{a\sqrt 3 }}{2}\)
Vì \(\left( {ABC} \right)\parallel \left( {A'B'C'} \right)\) nên \(d\left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) = d\left( {A',\left( {ABC} \right)} \right) = A'H = \frac{{a\sqrt 3 }}{2}\)
Mục 5 trong SGK Toán 11 tập 2 Cánh Diều tập trung vào các kiến thức về đường thẳng và mặt phẳng trong không gian. Đây là một phần quan trọng, đặt nền móng cho các kiến thức hình học không gian phức tạp hơn ở các lớp trên. Việc nắm vững các khái niệm, định lý và phương pháp giải bài tập trong mục này là rất cần thiết để đạt kết quả tốt trong môn Toán.
Bài 1 yêu cầu xác định vị trí tương đối giữa hai đường thẳng cho trước. Để giải bài tập này, các em cần sử dụng kiến thức về vectơ chỉ phương của hai đường thẳng. Nếu hai vectơ chỉ phương cùng phương, hai đường thẳng song song hoặc trùng nhau. Nếu hai vectơ chỉ phương không cùng phương và không vuông góc, hai đường thẳng cắt nhau. Nếu hai vectơ chỉ phương vuông góc, hai đường thẳng vuông góc.
Bài 2 yêu cầu tính góc giữa hai đường thẳng. Các em cần sử dụng công thức tính góc giữa hai đường thẳng dựa trên tích vô hướng của hai vectơ chỉ phương. Lưu ý rằng góc giữa hai đường thẳng luôn nhỏ hơn hoặc bằng 90 độ.
Bài 3 yêu cầu xác định góc giữa đường thẳng và mặt phẳng. Các em cần sử dụng công thức tính góc giữa đường thẳng và mặt phẳng dựa trên vectơ chỉ phương của đường thẳng và vectơ pháp tuyến của mặt phẳng. Lưu ý rằng góc giữa đường thẳng và mặt phẳng luôn nhỏ hơn hoặc bằng 90 độ.
Bài 4 yêu cầu tính khoảng cách từ một điểm đến mặt phẳng. Các em cần sử dụng công thức tính khoảng cách từ một điểm đến mặt phẳng dựa trên tọa độ của điểm và phương trình của mặt phẳng.
Bài 5 là một bài tập tổng hợp, yêu cầu các em vận dụng kiến thức về đường thẳng, mặt phẳng, góc và khoảng cách để giải quyết một bài toán thực tế. Để giải bài tập này, các em cần phân tích kỹ đề bài, xác định các yếu tố cần thiết và áp dụng các công thức phù hợp.
Hy vọng với lời giải chi tiết và những lời khuyên hữu ích trên đây, các em sẽ tự tin hơn trong việc học tập và giải bài tập Toán 11 chương trình Cánh Diều. Chúc các em học tốt!