Bài 4 trang 109 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Cánh Diều, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này đòi hỏi học sinh phải nắm vững các công thức đạo hàm cơ bản và kỹ năng giải toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 4 trang 109, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin làm bài tập.
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.
Đề bài
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.
a) Chứng minh rằng (AFD) // (BEC)
b) Gọi M là trọng tâm của tam giác ABE. Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (AFD). Lấy N là giao điểm của (P) và AC. Tính \(\frac{{AN}}{{NC}}\)
Phương pháp giải - Xem chi tiết
Nếu mặt phẳng (P) chứa hai đường thằng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q)
Lời giải chi tiết
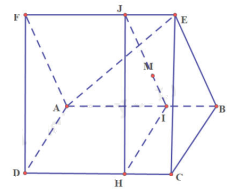
a) Ta có: AD // BC (ABCD là hình bình hành)
mà AD thuộc (AFD), BC thuộc (BEC)
nên (AFD) // (BEC)
b) Trong (ABEF), kẻ đường thẳng d qua M // AF
Ta có: d cắt AB tại I, d cắt EF tại J (1)
Trong (ABCD) có I thuộc (P) mà (P) // (AFD)
Suy ra từ I kẻ IH // AD (2)
Từ (1) và (2) suy ra: (IJH) trùng (P) và // (AFD)
Ta có: (P) cắt AC tại N mà AC thuộc (ABCD), IH thuộc (P) và (ABCD)
Suy ra IH cắt AC tại N
Ta có các hình bình hành IBCH, IBEJ
Gọi O là trung điểm của AB
Ta có M là trọng tâm của tam giác ABE
Suy ra \(\frac{{MO}}{{ME}} = \frac{1}{2}\)
Ta có AB // CD suy ra AI // CH
Định lý Ta – let:\(\frac{{AN}}{{NC}} = \frac{{AI}}{{CH}}\)
Mà CH = IB (IBCH là hình bình hành)
Suy ra\(\frac{{AN}}{{NC}} = \frac{{AI}}{{IB}}\)
Ta có: AB // EF nên OI // EJ
Do đó:\(\frac{{OI}}{{{\rm{EJ}}}} = \frac{{MO}}{{ME}} = \frac{1}{2}\)
Mà EJ = IB (IBEJ là hình bình hành)
Suy ra\(\frac{{OI}}{{IB}} = \frac{1}{2}\) hay\(IB = 2OI\)
Ta có\(\frac{{AN}}{{NC}} = \frac{{AI}}{{IB}} = \frac{{AO + OI}}{{2OI}}\)
Mà OA = OB (O là trung điểm AB)
Nên \(\frac{{AN}}{{NC}} = \frac{{OB + OI}}{{2OI}} = 2\)
Do đó: \(\frac{{AN}}{{NC}} = 2\)
Bài 4 trang 109 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học Toán 11, yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến tốc độ thay đổi của hàm số. Để giúp các em học sinh nắm vững kiến thức và tự tin giải bài tập, giaitoan.edu.vn xin giới thiệu lời giải chi tiết và hướng dẫn giải bài tập này.
Bài 4 trang 109 SGK Toán 11 tập 1 - Cánh Diều thường yêu cầu học sinh thực hiện các nhiệm vụ sau:
Để giải Bài 4 trang 109 SGK Toán 11 tập 1 - Cánh Diều, các em cần thực hiện theo các bước sau:
Ví dụ, xét bài tập sau:
Cho hàm số f(x) = x2 + 2x + 1. Tính f'(2).
Lời giải:
Khi giải Bài 4 trang 109 SGK Toán 11 tập 1 - Cánh Diều, các em cần lưu ý những điều sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Để luyện tập thêm, các em có thể giải các bài tập tương tự sau:
Bài 4 trang 109 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về đạo hàm và rèn luyện kỹ năng giải toán. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập mà giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong việc học tập môn Toán.
| Công thức đạo hàm | Ví dụ |
|---|---|
| (xn)' = nxn-1 | (x2)' = 2x |
| (sin x)' = cos x | (sin x)' = cos x |
| (cos x)' = -sin x | (cos x)' = -sin x |