Chào mừng các em học sinh đến với lời giải chi tiết Bài 2 trang 31 SGK Toán 11 tập 1 - Cánh diều. Bài học này thuộc chương trình đại số lớp 11, tập trung vào việc vận dụng các kiến thức về hàm số và đồ thị để giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp lời giải chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng (left( { - pi ;frac{{3pi }}{2}} right)) để:
Đề bài
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\) để:
a) Hàm số y = tanx nhận giá trị bằng – 1
b) Hàm số y = tanx nhận giá trị bằng 0
c) Hàm số y = cotx nhận giá trị bằng 1
d) Hàm số y = cotx nhận giá trị bằng 0
Phương pháp giải - Xem chi tiết
Sử dụng đồ thị hàm số.
Lời giải chi tiết
a) Hàm số y = tanx nhận giá trị bằng – 1
- Vẽ hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = - 1
- Lấy giao điểm của hai hàm số y = tanx và y = - 1
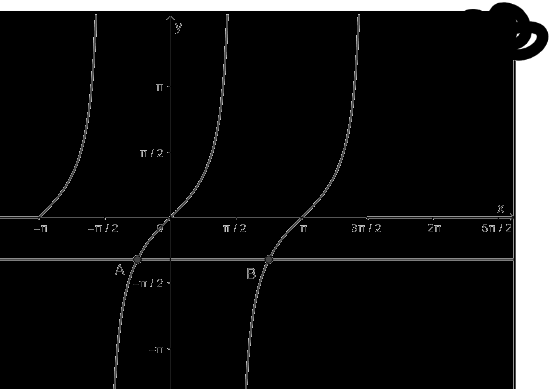
b) Hàm số y = tanx nhận giá trị bằng 0
- Vẽ hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = tanx và y = 0
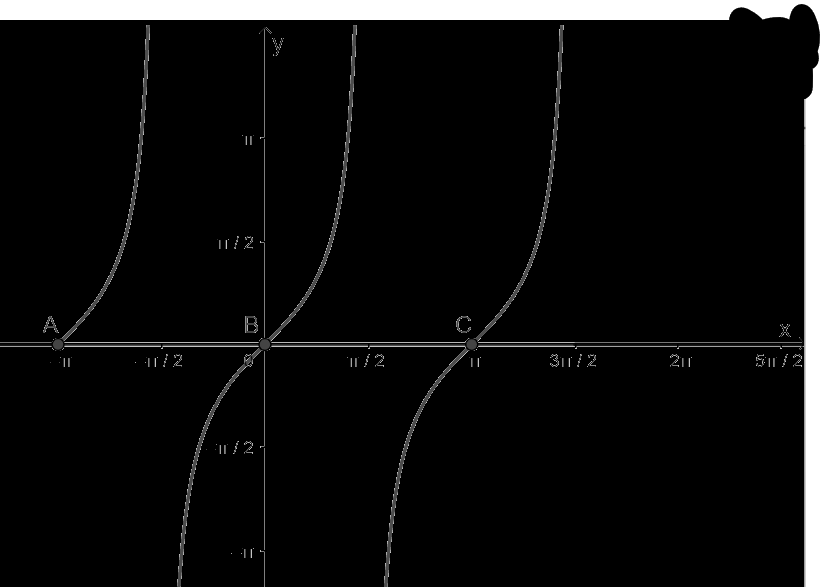
c) Hàm số y = cotx nhận giá trị bằng 1
- Vẽ hàm số y = cotx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 1
- Lấy giao điểm của hai hàm số y = cotx và y = 1
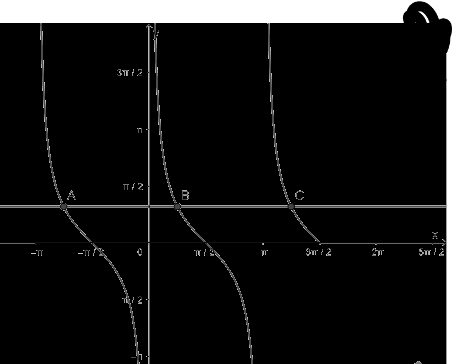
d) Hàm số y = cotx nhận giá trị bằng 0
- Vẽ hàm số y = cotx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = tanx và y = 0
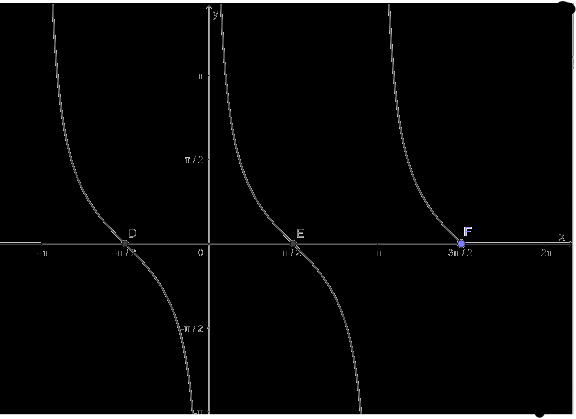
Bài 2 trang 31 SGK Toán 11 tập 1 - Cánh diều là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về hàm số bậc hai và ứng dụng của nó. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài 2 yêu cầu học sinh xác định tập xác định của hàm số và tính giá trị của hàm số tại một số điểm cho trước. Cụ thể, bài tập có thể bao gồm các hàm số sau:
Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Ví dụ 1: Xác định tập xác định của hàm số y = (x + 1) / (x - 2)
Lời giải: Hàm số y = (x + 1) / (x - 2) xác định khi và chỉ khi mẫu số x - 2 khác 0. Do đó, x ≠ 2. Vậy tập xác định của hàm số là D = R \ {2}.
Ví dụ 2: Tính giá trị của hàm số y = x2 - 3x + 2 tại x = 1
Lời giải: Thay x = 1 vào biểu thức của hàm số, ta được: y = 12 - 3(1) + 2 = 1 - 3 + 2 = 0. Vậy giá trị của hàm số tại x = 1 là 0.
Để luyện tập thêm, các em có thể giải các bài tập tương tự sau:
Khi giải bài tập về hàm số, các em cần lưu ý những điều sau:
Hàm số có rất nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em sẽ hiểu rõ hơn về Bài 2 trang 31 SGK Toán 11 tập 1 - Cánh diều và có thể tự tin giải các bài tập tương tự. Chúc các em học tập tốt!