Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 4 trang 37 SGK Toán 11 tập 1 - Cánh Diều. Bài viết này cung cấp đáp án đầy đủ, chính xác, cùng với phương pháp giải rõ ràng, giúp học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Quan sát giao điểm của đồ thị hàm số y = tanx và đường thẳng y = m (Hình 36).
Quan sát giao điểm của đồ thị hàm số y = tan x và đường thẳng y = 1
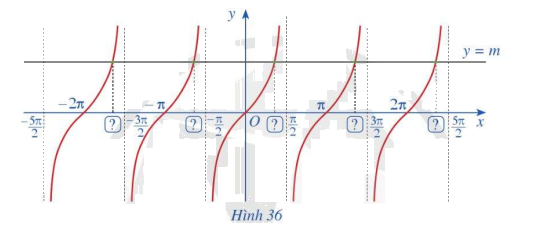
a) Từ hoành độ giao điểm của đồ thị hàm số y = tanx và đường thẳng y = m trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\), hãy xác định tất cả các hoành độ giao điểm của hai đồ thị đó
b) Có nhận xét gì về nghiệm của phương trình tanx = 1
Phương pháp giải:
Dựa vào phương trình lượng giác của sinx và cosx để làm bài
Lời giải chi tiết:
a) Do hoành độ giao điểm nằm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) nên: \(\tan x = m \Leftrightarrow \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \)
b) Nhận xét: trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\), với mọi \(m \in \mathbb{R}\) ta luôn có \(x = \alpha + k\pi \)
a) Giải phương trình \(\tan x = 1\)
b) Tìm góc lượng giác x saoo cho \(\tan x = \tan {67^ \circ }\)
Phương pháp giải:
Sử dụng công thức tổng quát để giải phương trình tan
Lời giải chi tiết:
a) \(\tan x = 1 \Leftrightarrow \tan x = \tan \frac{\pi }{4} \Leftrightarrow x = \frac{\pi }{4} + k\pi \)
b) \(\tan x = \tan {67^ \circ } \Leftrightarrow x = {67^ \circ } + k{.180^ \circ }\)
Mục 4 trang 37 SGK Toán 11 tập 1 - Cánh Diều thuộc chương trình học về hàm số bậc hai. Đây là một phần quan trọng trong chương trình Toán 11, đòi hỏi học sinh phải nắm vững kiến thức về parabol, đỉnh, trục đối xứng, và các yếu tố ảnh hưởng đến hình dạng của parabol.
Mục 4 tập trung vào việc xét dấu tam thức bậc hai và ứng dụng vào giải các bài toán liên quan đến bất phương trình bậc hai. Cụ thể, học sinh sẽ được hướng dẫn:
Để giải tốt các bài tập trong Mục 4 trang 37, học sinh cần nắm vững các bước sau:
Đề bài: Xét dấu của tam thức f(x) = 2x2 - 5x + 2.
Giải:
| Khoảng | x < 1/2 | 1/2 < x < 2 | x > 2 |
|---|---|---|---|
| Dấu của f(x) | + | - | + |
Vậy, f(x) > 0 khi x < 1/2 hoặc x > 2, và f(x) < 0 khi 1/2 < x < 2.
Giaitoan.edu.vn là địa chỉ tin cậy dành cho học sinh, sinh viên và những người yêu thích môn Toán. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 11 tập 1 - Cánh Diều, cùng với nhiều tài liệu học tập hữu ích khác. Hãy truy cập giaitoan.edu.vn để học Toán 11 hiệu quả hơn!