Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 tập 2. Chúng tôi giúp bạn nắm vững kiến thức và tự tin giải quyết các bài toán trong sách giáo khoa Cánh Diều.
Mục 6 trang 87 SGK Toán 11 tập 2 tập trung vào các kiến thức quan trọng về... (Nội dung tiếp theo sẽ được trình bày chi tiết trong bài viết bên dưới)
Trong Hình 27, mặt sàn gợi nên hình ảnh mặt phẳng (P), đường thẳng a không vuông góc với mặt phẳng (P)
Trong Hình 27, mặt sàn gợi nên hình ảnh mặt phẳng (P), đường thẳng a không vuông góc với mặt phẳng (P), đường thẳng a’ là hình chiếu của đường thẳng a trên mặt phẳng (P), đường thẳng d nằm trong mặt phẳng (P). Quan sát Hình 27 và cho biết:
a) Nếu đường thẳng d vuông góc với hình chiếu a’ thì đường thẳng d có vuông góc với a hay không?
b) Ngược lại, nếu dường thẳng d vuông góc với a thì đường thẳng d có vuông góc với hình chiếu a’ hay không
Phương pháp giải:
Quan sát hình vẽ để trả lời
Lời giải chi tiết:
Gọi A, B là 2 điểm phân biệt thuộc a
Gọi A’, B’ lần lượt là hình chiếu của A và B trên (P)
a) Vì \(d \subset \left( P \right)\) nên \(d \bot AA'\)
Vậy nếu \(d \bot a'\) thì \(d \bot mp\left( {a,a'} \right)\) do đó \(d \bot a\)
b) Ngược lại, nếu \(d \bot a\) thì \(d \bot mp\left( {a,a'} \right)\) do đó \(d \bot a'\)
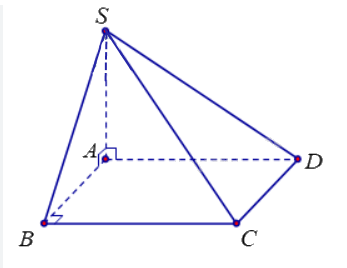
Cho hình chóp S.ABCD có \(SA \bot (ABCD)\) và đáy ABCD là hình chữ nhật. Chứng minh rằng các tam giác SBC và SCD là các tam giác vuông
Phương pháp giải:
Để chứng minh một tam giác là tam giác vuông ta chứng minh tam giác đó có một góc bằng 90o. Hoặc chứng minh tam giác có 2 cạnh vuông góc với nhau.
Lời giải chi tiết:

Vì ABCD là hình chữ nhật nên \(BC \bot AB\).
Vì \(SA \bot (ABCD) \Rightarrow SA \bot AB,\,SA \bot CD\)
+ Ta có:
\(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\\AB \cap SA = A\\AB,\,SA \subset (SAB)\end{array} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot SB\)
Xét \(\Delta SBC\) có \(BC \bot SB \Rightarrow \)Tam giác SBC vuông tại B.
+ Ta có:
\(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\\AD \cap SA = A\\AD,\,SA \subset (SAD)\end{array} \right. \Rightarrow CD \bot (SAD) \Rightarrow CD \bot SD\)
Xét \(\Delta SCD\) có \(CD \bot SD \Rightarrow \)Tam giác SCD vuông tại D.
Mục 6 trang 87 SGK Toán 11 tập 2 - Cánh Diều là một phần quan trọng trong chương trình học, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Việc nắm vững các khái niệm và phương pháp giải quyết bài tập trong mục này là nền tảng vững chắc cho việc học tập các kiến thức nâng cao hơn trong chương trình Toán 11.
Mục 6 trang 87 thường bao gồm các dạng bài tập sau:
Để giải các bài tập về đạo hàm, cần nắm vững các công thức đạo hàm cơ bản và quy tắc tính đạo hàm của hàm hợp. Ví dụ:
Khi tính đạo hàm của hàm hợp, cần sử dụng quy tắc đạo hàm của hàm hợp: y' = (y')u * (u')x
Để tìm cực trị của hàm số, cần giải phương trình y' = 0 và xét dấu đạo hàm cấp hai. Nếu đạo hàm cấp hai dương tại một điểm, điểm đó là điểm cực tiểu. Nếu đạo hàm cấp hai âm tại một điểm, điểm đó là điểm cực đại.
Để khảo sát hàm số, cần xác định tập xác định, các điểm gián đoạn, các điểm cực trị, các điểm uốn và vẽ đồ thị hàm số.
Để tìm phương trình tiếp tuyến của đường cong tại một điểm, cần xác định hệ số góc của tiếp tuyến bằng đạo hàm của hàm số tại điểm đó. Sau đó, sử dụng công thức phương trình đường thẳng đi qua một điểm với hệ số góc cho trước để tìm phương trình tiếp tuyến.
Ví dụ 1: Tính đạo hàm của hàm số y = x2 + 2x - 1
Giải:y' = 2x + 2
Ví dụ 2: Tìm cực trị của hàm số y = x3 - 3x2 + 2
Giải:y' = 3x2 - 6x. Giải phương trình y' = 0 ta được x = 0 hoặc x = 2. y'' = 6x - 6. Tại x = 0, y'' = -6 < 0, hàm số đạt cực đại tại x = 0. Tại x = 2, y'' = 6 > 0, hàm số đạt cực tiểu tại x = 2.
Để học tốt Mục 6 trang 87 SGK Toán 11 tập 2 - Cánh Diều, bạn nên:
Giải mục 6 trang 87 SGK Toán 11 tập 2 - Cánh Diều đòi hỏi sự hiểu biết vững chắc về đạo hàm và các ứng dụng của nó. Bằng cách nắm vững các kiến thức và phương pháp giải quyết bài tập, bạn có thể tự tin giải quyết các bài toán trong sách giáo khoa và các bài tập nâng cao khác.