Bài 6 trang 77 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 tập 1, Cánh Diều. Bài tập này yêu cầu học sinh vận dụng kiến thức về phép biến hóa affine để giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
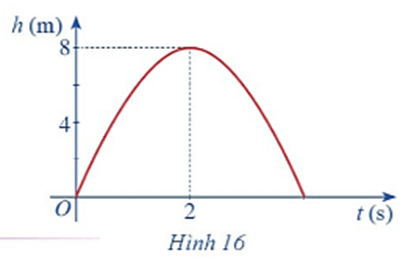
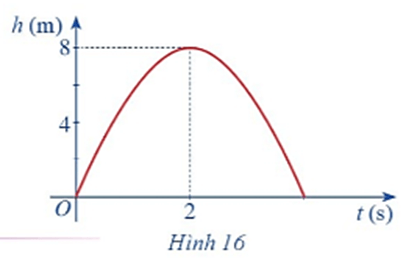
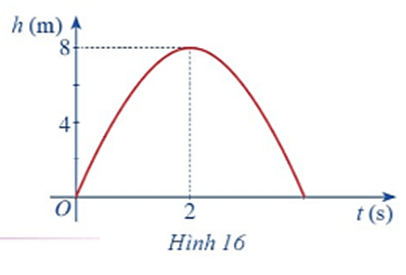
Hình 16 biểu thị độ cao h (m) của một quả bóng được đá lên theo thời gian t (s), trong đó \(h\left( t \right) = - 2{t^2} + 8t.\) a) Chứng tỏ hàm số \(h\left( t \right)\) liên tục trên tập xác định. b) Dựa vào đồ thị hãy xác định \(\mathop {\lim }\limits_{t \to 2} \left( { - 2{t^2} + 8t} \right).\)
Đề bài
Hình 16 biểu thị độ cao h (m) của một quả bóng được đá lên theo thời gian t (s), trong đó \(h\left( t \right) = - 2{t^2} + 8t.\)
a) Chứng tỏ hàm số \(h\left( t \right)\) liên tục trên tập xác định.
b) Dựa vào đồ thị hãy xác định \(\mathop {\lim }\limits_{t \to 2} \left( { - 2{t^2} + 8t} \right).\)
Phương pháp giải - Xem chi tiết
Các hàm đa thức liên tục trên \(\mathbb{R}\)
Lời giải chi tiết
a) Hàm số \(h\left( t \right) = - 2{t^2} + 8t\) là hàm đa thức nên liên tục trên \(\mathbb{R}\) do đó hàm số \(h\left( t \right)\) liên tục trên tập xác định.
b) Dựa vào đồ thị hàm số khi t tiến dần đến 2 thì h(t) dần đến 8.
Vậy \(\mathop {\lim }\limits_{t \to 2} \left( { - 2{t^2} + 8t} \right) = 8\)
Bài 6 trang 77 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc củng cố kiến thức về phép biến hóa affine. Để giải bài tập này, học sinh cần nắm vững định nghĩa, tính chất của phép biến hóa affine và cách xác định ma trận của phép biến hóa affine.
Bài 6 yêu cầu học sinh thực hiện các nhiệm vụ sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi xin trình bày lời giải chi tiết như sau:
Phép biến hóa affine là một phép biến đổi hình học bảo toàn tính thẳng hàng và tỷ lệ của các đoạn thẳng. Một phép biến hóa affine được xác định bởi một ma trận vuông cấp n và một vector tịnh tiến.
Ma trận của phép biến hóa affine đóng vai trò quan trọng trong việc xác định ảnh của một điểm qua phép biến hóa affine. Để tìm ma trận của phép biến hóa affine, ta cần xác định các điểm tương ứng và giải hệ phương trình tuyến tính.
Câu a: Cho hai điểm A(1; 2) và B(3; 4). Tìm phép biến hóa affine f biến A thành A'(-1; 0) và B thành B'(5; 2).
Lời giải: Gọi ma trận của phép biến hóa affine f là M = [[a, b], [c, d]] và vector tịnh tiến là [[x0], [y0]]. Ta có:
[[a, b], [c, d]] * [[1], [2]] + [[x0], [y0]] = [[-1], [0]]
[[a, b], [c, d]] * [[3], [4]] + [[x0], [y0]] = [[5], [2]]
Giải hệ phương trình này, ta tìm được a, b, c, d, x0, y0.
Câu b: ... (Giải tương tự như câu a)
Phép biến hóa affine có nhiều ứng dụng trong thực tế, đặc biệt trong lĩnh vực đồ họa máy tính, xử lý ảnh và robot học. Nó được sử dụng để thực hiện các phép biến đổi hình học như tịnh tiến, quay, co giãn và cắt.
Để củng cố kiến thức về phép biến hóa affine, học sinh có thể làm thêm các bài tập tương tự trong SGK Toán 11 tập 1 - Cánh Diều và các tài liệu tham khảo khác.
Bài 6 trang 77 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng giúp học sinh hiểu sâu hơn về phép biến hóa affine. Hy vọng với lời giải chi tiết và hướng dẫn của chúng tôi, học sinh có thể tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.