Chào mừng các em học sinh đến với lời giải chi tiết Bài 3 trang 31 SGK Toán 11 tập 1 - Cánh diều. Bài viết này sẽ cung cấp cho các em những kiến thức cần thiết và phương pháp giải bài tập hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, giúp các em học tập tốt hơn và đạt kết quả cao trong các kỳ thi.
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:
Đề bài
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:
a) y = sinx trên khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right),\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
b) y = cosx trên khoảng \(\left( { - 20\pi ; - 19\pi } \right),\left( { - 9\pi ; - 8\pi } \right)\)
Phương pháp giải - Xem chi tiết
Sử dụng khoản biến thiên của hàm số sin x, cos x.
Lời giải chi tiết
a) y = sinx
- Khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
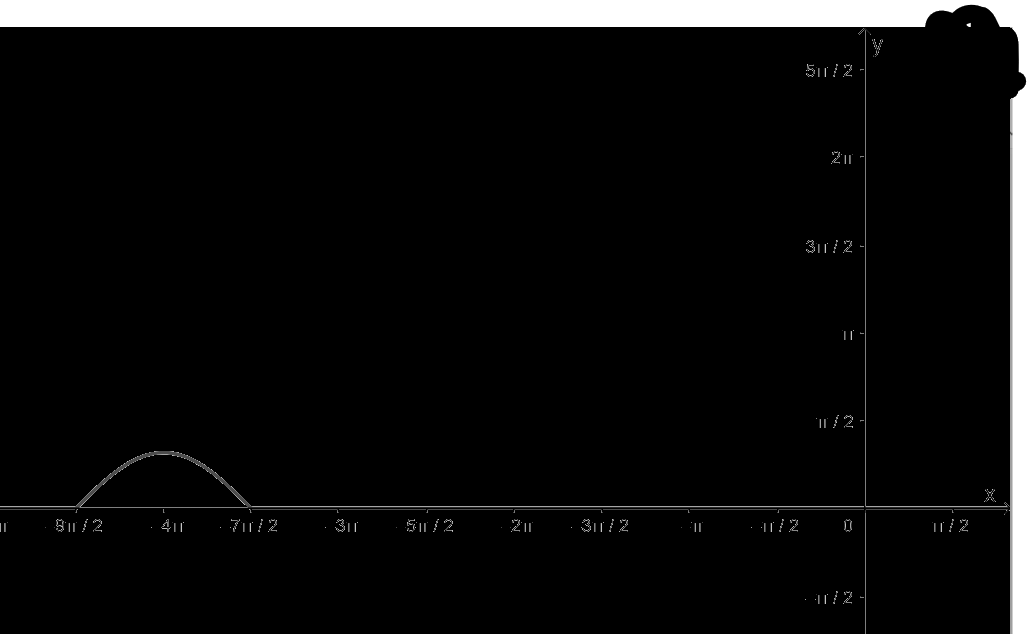
+ Đồng biến trên khoảng \(\left( { - \frac{{9\pi }}{2}; - 4\pi } \right)\)
+ Nghịch biến trên khoảng; \(\left( { - 4\pi ; - \frac{{7\pi }}{2}} \right)\)
- Khoảng \(\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
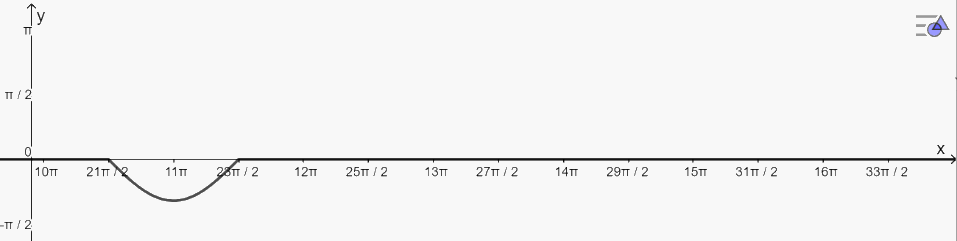
+ Đồng biến trên khoảng: \(\left( {11\pi ;\frac{{23\pi }}{2}} \right)\)
+ Nghịch biến trên khoảng: \(\left( {\frac{{21\pi }}{2};11\pi } \right)\)
b) Xét hàm số \(y = \cos x\):
Do \(\left( { - 20\pi ; - 19\pi } \right) = \left( {0 - 20\pi ;\pi - 20\pi } \right)\)nên hàm số \(y = \cos x\) nghịch biến trên khoảng \(\left( { - 20\pi ; - 19\pi } \right)\)
Do \(\left( { - 9\pi ; - 8\pi } \right) = \left( { - \pi - 8\pi ;0 - 8\pi } \right)\) nên hàm số \(y = \cos x\) đồng biến trên khoảng \(\left( { - 9\pi ; - 8\pi } \right)\)
Bài 3 trang 31 SGK Toán 11 tập 1 - Cánh diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về hàm số bậc hai và đồ thị của hàm số bậc hai. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Bài 3 thường bao gồm các dạng bài tập sau:
Để giải quyết từng dạng bài tập, chúng ta cần áp dụng các công thức và phương pháp sau:
Hàm số bậc hai có dạng y = ax2 + bx + c. Để xác định hệ số a, b, c, ta chỉ cần so sánh hàm số đã cho với dạng tổng quát này. Ví dụ, nếu hàm số là y = 2x2 - 3x + 1, thì a = 2, b = -3, c = 1.
Tọa độ đỉnh của parabol có dạng I(x0, y0), trong đó:
Ví dụ, với hàm số y = 2x2 - 3x + 1, ta có:
Vậy tọa độ đỉnh của parabol là I(3/4, -1/8).
Để vẽ đồ thị của hàm số bậc hai, ta thực hiện các bước sau:
Nếu biết giá trị x, ta thay vào hàm số để tìm giá trị y tương ứng. Ngược lại, nếu biết giá trị y, ta giải phương trình bậc hai để tìm giá trị x tương ứng.
Cho hàm số y = x2 - 4x + 3. Hãy tìm tọa độ đỉnh và vẽ đồ thị của hàm số.
Giải:
Vẽ parabol đi qua các điểm I(2, -1), A(0, 3), B(1, 0) và C(3, 0).
Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin giải quyết Bài 3 trang 31 SGK Toán 11 tập 1 - Cánh diều một cách hiệu quả. Chúc các em học tập tốt!