Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết các bài tập trong mục 2 trang 6 SGK Toán 11 tập 2 - Cánh Diều.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Xét mẫu số liệu trong Ví dụ 2 được cho dưới dạng bảng tần số ghép nhóm (Bảng 7).
Xét mẫu số liệu trong Ví dụ 2 được cho dưới dạng bảng tần số ghép nhóm (Bảng 4).
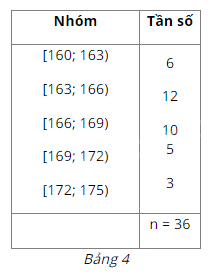
a) Tìm trung điểm \({x_1}\) của nửa khoảng (tính bằng trung bình cộng của hai đầu mút) ứng với nhóm 1. Ta gọi trung điểm \({x_1}\) là giá trị đại diện của nhóm 1.
b) Bằng cách tương tự, hãy tìm giá trị đại diện của bốn nhóm còn lại. Từ đó, hãy hoàn thiện các số liệu trong Bảng 7.
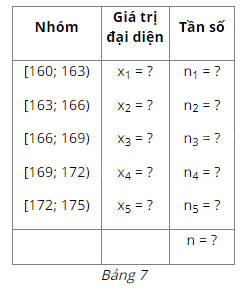
c) Tính giá trị \(\overline x \) cho bởi công thức sau:
\(\overline x = \frac{{{n_1}{x_1} + {n_2}{x_2} + ... + {n_5}{x_5}}}{n}\)
Phương pháp giải:
- Tìm trung điểm bằng cách lấy hai đầu mút cộng lại chia 2
- Tìm \(\overline x \) bằng công thức đã cho
Lời giải chi tiết:
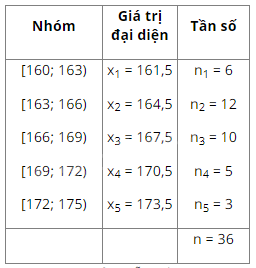
c) Số trung bình cộng của mẫu số liệu đã cho là:
\[\bar{x}=\frac{6\cdot 161,5+12\cdot 164,5+10\cdot 167,5+5\cdot 170,5+3\cdot 173,5}{36}=166,41(6)\]
Xác định số trung bình cộng của mẫu số liệu ghép nhóm trong bài toán ở Luyện tập 2
Phương pháp giải:
Dựa vào kiến thức trung vị vừa học để xác định
Lời giải chi tiết:
Trung điểm \({x_1} = 29,5\) là giá trị đại diện của nhóm 1
Trung điểm \({x_2} = 38,5\) là giá trị đại diện của nhóm 2
Trung điểm \({x_3} = 47,5\) là giá trị đại diện của nhóm 3
Trung điểm \({x_4} = 56,5\) là giá trị đại diện của nhóm 4
Trung điểm \({x_5} = 65,5\) là giá trị đại diện của nhóm 5
Trung điểm \({x_6} = 74,5\) là giá trị đại diện của nhóm 6
Trung điểm \({x_7} = 83,5\) là giá trị đại diện của nhóm 7
Trung điểm \({x_8} = 92,5\) là giá trị đại diện của nhóm 8
\({n_1} = 3;{n_2} = 3;{n_3} = 6;{n_4} = 5;{n_5} = 4;{n_6} = 3;{n_7} = 4;{n_8} = 2\)
\( \Rightarrow \overline x = \frac{{29,5.3 + 38,5.3 + 47,5.6 + 56,5.5 + 65,5.4 + 74,5.3 + 83,5.4 + 92,5.2}}{{30}} = 59,2\)
Mục 2 trang 6 SGK Toán 11 tập 2 - Cánh Diều tập trung vào việc ôn tập chương 3: Hàm số lượng giác và ứng dụng của hàm số lượng giác. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức về định nghĩa, tính chất của hàm số lượng giác, các phép biến đổi lượng giác và giải phương trình lượng giác cơ bản.
Mục 2 bao gồm các bài tập trắc nghiệm và tự luận, được thiết kế để kiểm tra mức độ hiểu bài và khả năng vận dụng kiến thức của học sinh. Dưới đây là phân tích chi tiết từng bài tập:
Bài 1 thường là các câu hỏi trắc nghiệm về định nghĩa, tính chất của hàm số lượng giác. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản và biết cách áp dụng chúng vào các tình huống cụ thể.
Bài 2 thường yêu cầu học sinh chứng minh các đẳng thức lượng giác hoặc giải phương trình lượng giác. Để giải bài tập này, học sinh cần sử dụng các công thức lượng giác cơ bản và các phương pháp giải phương trình lượng giác đã học.
Để giải các bài tập trong mục 2 trang 6 SGK Toán 11 tập 2 - Cánh Diều một cách hiệu quả, học sinh cần nắm vững các công thức lượng giác sau:
| Công thức | Mô tả |
|---|---|
| sin2(x) + cos2(x) = 1 | Đẳng thức lượng giác cơ bản |
| tan(x) = sin(x) / cos(x) | Công thức tính tan(x) |
| cot(x) = cos(x) / sin(x) | Công thức tính cot(x) |
Khi gặp các phương trình lượng giác, học sinh có thể sử dụng các phương pháp sau:
Để nắm vững kiến thức và kỹ năng giải toán, học sinh nên luyện tập thường xuyên với các bài tập khác nhau. Ngoài ra, học sinh có thể tham khảo các tài liệu tham khảo, các bài giảng online hoặc tìm kiếm sự giúp đỡ từ giáo viên và bạn bè.
Khi giải bài tập, học sinh nên:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 2 trang 6 SGK Toán 11 tập 2 - Cánh Diều. Chúc bạn học tập tốt!