Bài 4 trang 31 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Cánh diều, tập trung vào việc vận dụng các kiến thức về giới hạn của hàm số để giải quyết các bài toán cụ thể. Bài tập này đòi hỏi học sinh phải nắm vững định nghĩa, tính chất của giới hạn và các phương pháp tính giới hạn thường gặp.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải bài tập Toán 11 một cách hiệu quả.
Dùng đồ thị hàm số, hãy cho biết:
Đề bài
Dùng đồ thị hàm số, hãy cho biết:
a) Với mỗi \(m \in \left[ { - 1;1} \right]\), có bao nhiêu giá trị \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\sin \alpha = m\)
b) Với mỗi \(m \in \left[ { - 1;1} \right]\), có bao nhiêu giá trị \(\alpha \in \left[ {0;\pi } \right]\) sao cho \(\cos \alpha = m\)
c) Với mỗi \(m \in \mathbb{R}\), có bao nhiêu giá trị \(\alpha \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) sao cho \(\tan \alpha = m\)
d) Với mỗi \(m \in \mathbb{R}\), có bao nhiêu giá trị \(\alpha \in \left( {0;\pi } \right)\) sao cho \(\cot \alpha = m\)
Phương pháp giải - Xem chi tiết
Sử dụng đồ thị của hàm số sin , cos , tan , cot
Lời giải chi tiết
a) Đồ thị hàm số:
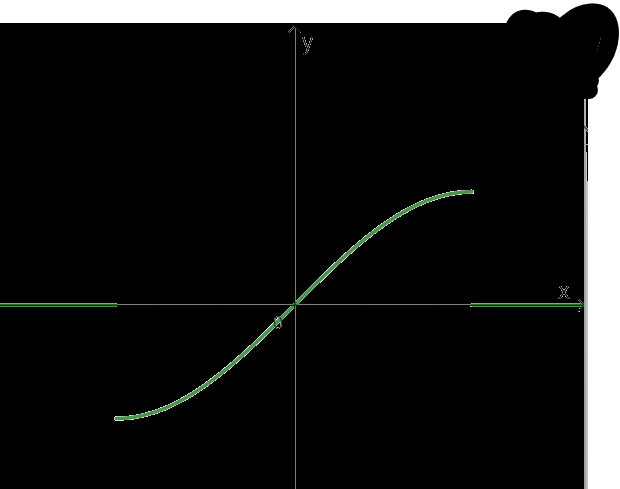
- Với mỗi \(m \in \left[ { - 1;1} \right]\) chỉ có 1 giá trị \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\sin \alpha = m\)
b) Đồ thị hàm số:
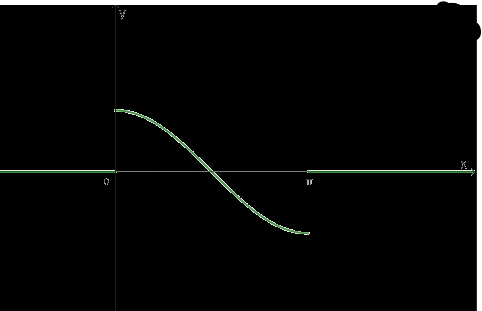
- Với mỗi \(m \in \left[ { - 1;1} \right]\) có 1 giá trị \(\alpha \in \left[ {0;\pi } \right]\) sao cho \(\cos \alpha = m\)
c) Đồ thị hàm số:
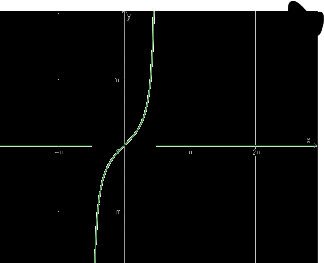
- Với mỗi \(m \in \mathbb{R}\), có 2 giá trị \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\tan \alpha = m\)
d) Đồ thị hàm số:
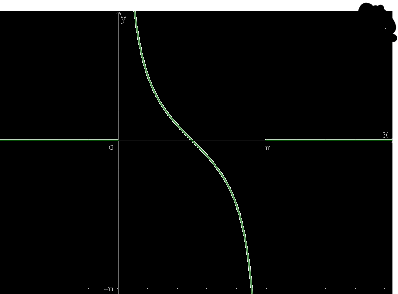
- Với mỗi \(m \in \mathbb{R}\), có 2 giá trị \(\alpha \in \left[ {0;\pi } \right]\) sao cho \(\cot \alpha = m\)
Bài 4 trang 31 SGK Toán 11 tập 1 - Cánh diều yêu cầu học sinh tính giới hạn của hàm số tại một điểm. Để giải bài tập này, chúng ta cần nắm vững các khái niệm cơ bản về giới hạn, bao gồm định nghĩa giới hạn, các tính chất của giới hạn và các phương pháp tính giới hạn.
Đề bài thường yêu cầu tính giới hạn của một hàm số khi x tiến tới một giá trị cụ thể. Ví dụ:
Có nhiều phương pháp để tính giới hạn, tùy thuộc vào dạng của hàm số. Một số phương pháp thường được sử dụng bao gồm:
Ví dụ 1: Tính lim (x→2) (x^2 - 4) / (x - 2)
Ta có thể phân tích thành nhân tử tử số như sau: x^2 - 4 = (x - 2)(x + 2). Do đó:
lim (x→2) (x^2 - 4) / (x - 2) = lim (x→2) (x - 2)(x + 2) / (x - 2) = lim (x→2) (x + 2) = 2 + 2 = 4
Ví dụ 2: Tính lim (x→0) sin(x) / x
Đây là một giới hạn đặc biệt, ta có: lim (x→0) sin(x) / x = 1
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Khi giải bài tập về giới hạn, cần lưu ý những điều sau:
Hy vọng với lời giải chi tiết và phân tích chuyên sâu này, các em học sinh sẽ hiểu rõ hơn về Bài 4 trang 31 SGK Toán 11 tập 1 - Cánh diều và có thể tự tin giải quyết các bài tập tương tự. giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.