Bài 8 trang 72 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Cánh Diều, tập trung vào việc giải các bài toán liên quan đến đạo hàm của hàm số. Bài học này giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng vào giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong Bài 8, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
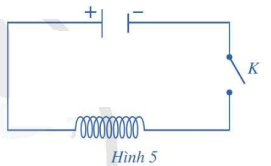
Cho mạch điện như Hình 5. Lúc đầu tụ điện có điện tích ({Q_0})
Đề bài
Cho mạch điện như Hình 5. Lúc đầu tụ điện có điện tích \({Q_0}\). Khi đóng khóa K, tụ điện phóng điện qua cuộn dây; điện tích q của tụ điện phụ thuộc vào thời gian t theo công thức \(q(t) = {Q_0}\sin \omega t\), trong đó \(\omega \) là tốc độ góc. Biết rằng cường độ I(t) của dòng diện tại thời điểm t được tính theo công thức \(I(t) = q'(t)\). Cho biết \({Q_0} = {10^{ - 8}}(C)\) và \(\omega = {10^6}\pi \,\,\,(rad/s)\). Tính cường độ của dòng điện tại thời điểm \(t = 6(s)\) (tính chính xác đến \({10^{ - 5}}(mA)\)
Phương pháp giải - Xem chi tiết
Dựa vào công thức đề bài cho để tìm đạo hàm sau đó tính
Lời giải chi tiết
\(I(t) = q'(t) = \left( {{Q_0}\sin \omega t} \right)' = {Q_o}.\omega .\cos \omega t\)
Cường độ của dòng điện tại thời điểm t = 6(s) là:
\(I(6) = {Q_o}\,.\,\omega \,.\,\cos \omega t = {10^{ - 8}}{.10^6}\pi .\cos {10^6}\pi .6 = 0,01\pi \,\,(A)\)
Bài 8 trong SGK Toán 11 tập 2 Cánh Diều yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến tính đạo hàm của hàm số, xét tính đơn điệu của hàm số và tìm cực trị. Để giúp học sinh hiểu rõ hơn về nội dung bài học, chúng tôi xin trình bày lời giải chi tiết cho từng bài tập.
Bài 8.1 yêu cầu tính đạo hàm của các hàm số sau:
Lời giải:
Bài 8.2 yêu cầu tìm đạo hàm của hàm số y = f(x) tại x = x0, biết:
f(x) = x2 + 5x - 3 và x0 = 2
Lời giải:
f'(x) = 2x + 5
f'(2) = 2(2) + 5 = 9
Bài 8.3 yêu cầu tìm đạo hàm của hàm số y = f(x) tại x = x0, biết:
f(x) = (x3 - 2x + 1) / (x + 1) và x0 = 0
Lời giải:
f'(x) = [(3x2 - 2)(x + 1) - (x3 - 2x + 1)(1)] / (x + 1)2
f'(0) = [(3(0)2 - 2)(0 + 1) - (03 - 2(0) + 1)(1)] / (0 + 1)2 = -2 - 1 = -3
Bài 8.4 yêu cầu tìm đạo hàm của hàm số y = f(x) tại x = x0, biết:
f(x) = √(x2 + 1) và x0 = 1
Lời giải:
f'(x) = (1/2) * (x2 + 1)-1/2 * 2x = x / √(x2 + 1)
f'(1) = 1 / √(12 + 1) = 1 / √2 = √2 / 2
Kết luận:
Việc nắm vững các quy tắc tính đạo hàm và áp dụng chúng một cách linh hoạt là rất quan trọng để giải quyết các bài toán liên quan đến đạo hàm. Hy vọng với lời giải chi tiết trên, các em học sinh có thể hiểu rõ hơn về Bài 8 trang 72 SGK Toán 11 tập 2 Cánh Diều và tự tin giải các bài tập tương tự.
Ngoài ra, các em có thể tham khảo thêm các bài giảng và tài liệu học tập khác tại giaitoan.edu.vn để nâng cao kiến thức và kỹ năng giải toán.