Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 69, 70 SGK Toán 11 tập 1 - Cánh Diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Bài tập trong mục 2 tập trung vào các kiến thức quan trọng của chương trình Toán 11 tập 1.
Cho hai hàm số (fleft( x right) = {x^2} - 1,gleft( x right) = x + 1.) a) Tính (mathop {lim }limits_{x to 1} fleft( x right)) và (mathop {lim }limits_{x to 1} gleft( x right).) b) Tính (mathop {lim }limits_{x to 1} left[ {fleft( x right) + gleft( x right)} right])và so sánh (mathop {lim }limits_{x to 1} fleft( x right) + mathop {lim }limits_{x to 1} gleft( x right).) c) Tính (mathop {lim }limits_{x to 1} left[ {fleft( x right) - gleft( x
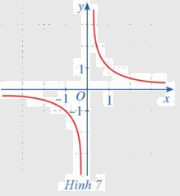
Cho hàm số \(f\left( x \right) = \frac{1}{x}\,\,\left( {x \ne 0} \right)\) có đồ thị như ở Hình 7. Quan sát đồ thị đó và cho biết:
a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới giá trị nào.
b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần tới giá trị nào.
Phương pháp giải:
Quan sát đồ thị Hình 7 để trả lời câu hỏi.
Lời giải chi tiết:
a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới 0.
b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần tới 0.
Tính \(\mathop {\lim }\limits_{x \to - \infty } \frac{{3x + 2}}{{4x - 5}}.\)
Phương pháp giải:
- Sử dụng \(\mathop {\lim }\limits_{x \to - \infty } \frac{c}{{{x^k}}} = 0;\mathop {\lim }\limits_{x \to - \infty } c = c\)
- Sử dụng các phép toán trên giới hạn.
Lời giải chi tiết:
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{3x + 2}}{{4x - 5}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{x\left( {3 + \frac{2}{x}} \right)}}{{x\left( {4 - \frac{5}{x}} \right)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{3 + \frac{2}{x}}}{{4 - \frac{5}{x}}} = \frac{{3 + 0}}{{4 - 0}} = \frac{3}{4}\)
Mục 2 của SGK Toán 11 tập 1 - Cánh Diều thường xoay quanh các chủ đề về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán 11.
Trang 69 SGK Toán 11 tập 1 - Cánh Diều thường chứa các bài tập về phép tịnh tiến. Các bài tập này yêu cầu học sinh xác định ảnh của một điểm, một đường thẳng, hoặc một hình qua phép tịnh tiến. Để giải các bài tập này, học sinh cần nắm vững công thức của phép tịnh tiến:
x' = x + a
y' = y + b
Trong đó:
Trang 70 SGK Toán 11 tập 1 - Cánh Diều thường chứa các bài tập về phép quay. Các bài tập này yêu cầu học sinh xác định ảnh của một điểm, một đường thẳng, hoặc một hình qua phép quay. Để giải các bài tập này, học sinh cần nắm vững công thức của phép quay:
x' = x.cos(α) - y.sin(α)
y' = x.sin(α) + y.cos(α)
Trong đó:
Bài tập: Cho điểm A(1, 2) và vectơ tịnh tiến v = (3, -1). Tìm tọa độ điểm A' là ảnh của điểm A qua phép tịnh tiến theo vectơ v.
Giải:
Áp dụng công thức phép tịnh tiến, ta có:
x' = 1 + 3 = 4
y' = 2 + (-1) = 1
Vậy, tọa độ điểm A' là (4, 1).
Việc giải các bài tập về phép biến hình đòi hỏi học sinh phải nắm vững kiến thức lý thuyết và kỹ năng vận dụng công thức. Hy vọng với lời giải chi tiết và các mẹo giải nhanh trên đây, các em học sinh sẽ tự tin hơn khi giải các bài tập trong SGK Toán 11 tập 1 - Cánh Diều.