Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1, trang 22, 23 và 24 sách giáo khoa Toán 11 tập 1 - Cánh Diều.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp những lời giải chính xác, khoa học, giúp các em nắm vững kiến thức và tự tin giải quyết các bài tập tương tự.
a) Cho hàm số (fleft( x right) = {x^2}) Với (x in mathbb{R}), hãy so sánh
a) Cho hàm số \(f\left( x \right) = {x^2}\)
Với \(x \in \mathbb{R}\), hãy so sánh \(f\left( { - x} \right)\) và \(f\left( x \right)\)
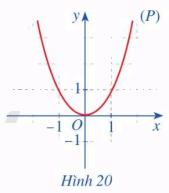
Quan sát parabol (P) là đồ thị của hàm số \(f\left( x \right) = {x^2}\) (Hình 20) và cho biết trục đối xứng của (P) là đường thẳng nào?
b) Cho hàm số \(g\left( x \right) = x\)
Với \(x \in \mathbb{R}\), hãy so sánh \(g\left( { - x} \right)\) và \(g\left( x \right)\)
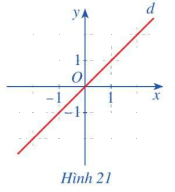
Quan sát đường thẳng d là đồ thị của hàm số \(g\left( x \right) = x\) (Hình 21) và cho biết gốc tọa độ O có là tâm đối xứng của đường thẳng d hãy không.
Phương pháp giải:
Dựa vào kiến thức về hàm số để xác định
Lời giải chi tiết:
a)
Ta có: \(f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2},f\left( x \right) = {x^2} \Rightarrow f\left( { - x} \right) = f\left( x \right)\)
Trục đối xứng của (P) là đường thẳng y = 0
b)
Ta có: \(g\left( { - x} \right) = - g\left( x \right)\)
Gốc tọa độ O là tâm đối xứng của đường thẳng d
a) Chứng tỏ rằng hàm số \(g(x) = {x^3}\)là hàm số lẻ.
b) Cho ví dụ về hàm số không là hàm số chẵn cũng không là hàm số lẻ.
Phương pháp giải:
Sử dụng định nghĩa hàm số chẵn, hàm số lẻ.

Lời giải chi tiết:
a)
Hàm số \(g(x) = {x^3}\)
+) Có tập xác định D = R;
+) Với mọi \(x \in R\)thì \( - x \in R\)
Ta có \(g( - x) = {\left( { - x} \right)^3} = - {x^3} = - g(x)\)
Vậy \(g(x) = {x^3}\)là hàm số lẻ.
b)
Ví dụ về hàm số không là hàm số chẵn không là hàm số lẻ là
\(f(x) = {x^3} + {x^2}\)
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có đồ thị như Hình 22.
a) Có nhận xét gì về đồ thị hàm số trên mỗi đoạn \(\left[ {a;a + T} \right],\left[ {a + T;a + 2T} \right],\left[ {a - T;a} \right]\)?

b) Lấy điểm \(M\left( {{x_0};f\left( {{x_0}} \right)} \right)\) thuộc đồ thị hàm số với \({x_0} \in \left[ {a;a + T} \right]\). So sánh mỗi giá trị \(f\left( {{x_0} + T} \right);f\left( {{x_0} - T} \right)\) với \(f\left( {{x_0}} \right)\)
Phương pháp giải:
Dựa vào cách nhìn đồ thị để trả lời câu hỏi
Lời giải chi tiết:
a) Đồ thị hàm số trên mỗi đoạn là như nhau
b) \(f\left( {{x_0} + T} \right) = f\left( {{x_0} - T} \right) = f\left( {{x_0}} \right)\)
Cho ví dụ về hàm số tuần hoàn
Phương pháp giải:
Sử dụng định nghĩa về hàm số tuần hoàn.
Lời giải chi tiết:
Ví dụ về hàm số tuần hoàn là : \(g(x) = \left\{ \begin{array}{l}0\,\,\,\,\,\,\,,x \in Q\\1\,\,\,\,\,\,\,\,,x \in R\end{array} \right.\)
Mục 1 của chương trình Toán 11 tập 1 - Cánh Diều tập trung vào việc ôn tập và mở rộng kiến thức về hàm số bậc hai. Các bài tập trong trang 22, 23 và 24 SGK Toán 11 tập 1 - Cánh Diều yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài tập này yêu cầu học sinh xác định hệ số a, b, c của hàm số bậc hai được cho dưới dạng tổng quát y = ax2 + bx + c. Để giải bài tập này, học sinh cần nắm vững định nghĩa của hàm số bậc hai và biết cách nhận biết các hệ số a, b, c.
Bài tập này yêu cầu học sinh tìm tập xác định của hàm số. Để giải bài tập này, học sinh cần nắm vững điều kiện xác định của hàm số và biết cách loại bỏ các giá trị làm mẫu số bằng 0 hoặc biểu thức dưới dấu căn âm.
Bài tập này yêu cầu học sinh vẽ đồ thị của hàm số bậc hai. Để giải bài tập này, học sinh cần xác định được đỉnh, trục đối xứng, điểm cắt trục Oy và một vài điểm khác trên đồ thị. Sau đó, vẽ đồ thị bằng cách nối các điểm đã xác định.
Trong quá trình giải bài tập, học sinh cần lưu ý một số điều sau:
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày ở trên, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong Mục 1 trang 22, 23, 24 SGK Toán 11 tập 1 - Cánh Diều. Chúc các em học tập tốt!