Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 4 trang 83, 84 SGK Toán 11 tập 2 - Cánh Diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán.
Bài tập trong mục này tập trung vào các kiến thức quan trọng của chương trình Toán 11, đòi hỏi các em phải có sự hiểu biết sâu sắc về lý thuyết và kỹ năng vận dụng linh hoạt.
Trong Hình 19, hai thanh sắt và bản phẳng để ngồi gợi nên hình ảnh hai đường thẳng a, b và mặt phẳng (P).
Trong Hình 19, hai thanh sắt và bản phẳng để ngồi gợi nên hình ảnh hai đường thẳng a, b và mặt phẳng (P). Quan sát Hình 19 và cho biết:
a) Nếu hai đường thẳng a và b song song với nhau và mặt phẳng (P) vuông góc với đường thẳng a thì mặt phẳng (P) có vuông góc với đường thẳng b hay không?
b) Nếu hai đường thẳng a và b cùng vuông góc với mặt phẳng (P) thì chúng có song song với nhau hay không?
Phương pháp giải:
Quan sát hình vẽ để trả lời
Lời giải chi tiết:
a, Gọi (Q) là mặt phẳng chứa đường thẳng a, b
Theo tính chất 2 “Có duy nhất 1 đường thẳng đi qua 1 điểm cho trước và vuông góc với một mặt phẳng cho trước”
b, Nếu hai đường thẳng a và b cùng vuông góc với mặt phẳng (P) thì chúng song song với nhau.
Cho đường thẳng d và mặt phẳng (P) cắt nhau tại điểm O. Lấy các điểm A, B thuộc d khác O; các điểm A', B' thuộc (P) thỏa mãn \(AA' \bot (P),\,BB' \bot (P)\). Chứng minh rằng: \(\frac{{AA'}}{{BB'}} = \frac{{OA}}{{OB}}\)
Phương pháp giải:
Sử dụng định lý Thalès: Nếu một đường thẳng song song với một cạnh của tam giác đó và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:

Do \({\rm{AA}}' \bot (P),\,BB' \bot (P) \Rightarrow {\rm{AA' //}}\,{\rm{BB'}}\)
Xét có \({\rm{AA' //}}\,{\rm{BB'}} \Rightarrow \frac{{{\rm{AA}}'}}{{{\rm{BB'}}}} = \frac{{OA}}{{OB}}\) (Định lý Thalès)
Trong Hình 21 , hai mặt sàn của nhà cao tầng và cột trụ bê tông gợi nên hình ảnh hai mặt phẳng (P), (Q) phân biệt và đường thẳng a.

Quan sát Hình 21 và cho biết:
a) Nếu hai mặt phẳng (P) và (Q) song song với nhau và đường thẳng a vuông góc với mặt phẳng (P) thì đường thẳng a có vuông góc với mặt phẳng (Q) hay không?
b) Nếu hai mặt phẳng (P) và (Q) cùng vuông góc với đường thẳng a thì chúng có song song với nhau hay không?
Phương pháp giải:
Quan sát hình vẽ để trả lời
Lời giải chi tiết:
a) Nếu (P) // (Q) và \(a \bot (P)\) thì \(a \bot (Q)\)
b) Nếu hai mặt phẳng (P) và (Q) cùng vuông góc với đường thẳng a thì chúng song song với nhau.
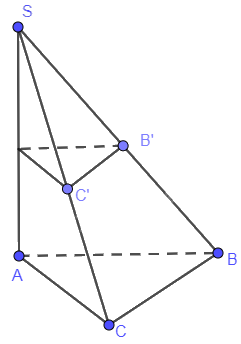
Cho hình chóp S.ABC có SA ⊥ (ABC). Mặt phẳng (P) khác với mặt phẳng (ABC), vuông góc với đường thẳng SA và lần lượt cắt các đường thẳng SB, SC tại hai điểm phân biệt B', C'. Chứng minh rằng B'C' // BC
Phương pháp giải:
Sử dụng tính chất: \(\left\{ \begin{array}{l}(P) \bot a\\(Q) \bot a\end{array} \right. \Rightarrow (P)\,//\,(Q)\)
Lời giải chi tiết:

Do \(\left\{ \begin{array}{l}(P) \bot SA\\(ABC) \bot SA\end{array} \right. \Rightarrow (P)\,//\,(ABC) \Rightarrow B'C'\,//BC\)
Mục 4 của SGK Toán 11 tập 2 - Cánh Diều thường xoay quanh các chủ đề về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các tính chất và ứng dụng của các phép biến hình này là vô cùng quan trọng, không chỉ cho việc giải các bài tập trong SGK mà còn là nền tảng cho các kiến thức toán học nâng cao hơn.
Phép tịnh tiến là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kỳ. Để giải các bài tập liên quan đến phép tịnh tiến, các em cần hiểu rõ định nghĩa, tính chất và công thức của phép tịnh tiến. Ví dụ, cho điểm A(x0, y0) và vector t = (a, b), ảnh của điểm A qua phép tịnh tiến theo vector t là điểm A'(x0 + a, y0 + b).
Phép quay là phép biến hình biến mỗi điểm thành một điểm khác sao cho khoảng cách từ điểm đó đến một điểm cố định (gọi là tâm quay) không đổi, và góc giữa hai đoạn thẳng nối điểm ban đầu và điểm ảnh với tâm quay là một góc cố định (gọi là góc quay). Các em cần nắm vững công thức tính tọa độ điểm ảnh sau phép quay quanh gốc tọa độ.
Phép đối xứng trục là phép biến hình biến mỗi điểm thành một điểm khác sao cho trục đối xứng là đường trung trực của đoạn thẳng nối điểm ban đầu và điểm ảnh. Để giải các bài tập về phép đối xứng trục, các em cần xác định đúng trục đối xứng và áp dụng công thức tính tọa độ điểm ảnh.
Phép đối xứng tâm là phép biến hình biến mỗi điểm thành một điểm khác sao cho tâm đối xứng là trung điểm của đoạn thẳng nối điểm ban đầu và điểm ảnh. Công thức tính tọa độ điểm ảnh sau phép đối xứng tâm cũng tương tự như phép đối xứng trục, nhưng thay vì trục đối xứng, chúng ta có tâm đối xứng.
Dưới đây là giải chi tiết các bài tập trong mục 4 trang 83, 84 SGK Toán 11 tập 2 - Cánh Diều:
Các phép biến hình có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, như:
Hy vọng với lời giải chi tiết và các mẹo giải nhanh trên đây, các em học sinh đã nắm vững kiến thức và kỹ năng giải các bài tập mục 4 trang 83, 84 SGK Toán 11 tập 2 - Cánh Diều. Chúc các em học tập tốt!