Chào mừng bạn đến với bài giải Bài 3 trang 119 SGK Toán 11 tập 1 - Cánh Diều trên giaitoan.edu.vn. Bài viết này cung cấp lời giải chi tiết, chính xác, giúp bạn hiểu rõ kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn học toán hiệu quả và đạt kết quả cao.
Vẽ hình biểu diễn của các vật trong Hình 89 và Hình 90.
Đề bài
Vẽ hình biểu diễn của các vật trong Hình 89 và Hình 90.

Phương pháp giải - Xem chi tiết
Để vẽ hình biểu diễn của một hình trong không gian, ta cần chú ý:
- Nếu trên hình H có hai đoạn thẳng cùng phương thì trên hình H’hình chiếu của hai đoạn thẳng đó phải cùng phương
- Trung điểm của một đoạn thẳng có hình chiếu là trung điểm của đoạn thẳng hình chiếu
- Trong tam giác có một góc tù, ta cần chú ý chân đường cao kẻ từ đỉnh của góc nhọn không nằm trên cạnh đối diện mà nằm ở phần trên kéo dài của cạnh ấy
- Một góc bất kỳ có thể biểu diễn cho mọi góc (nhọn, vuông, tù)
- Một tam giác bất kỳ có thể là hình biểu diễn của mọi tam giác (cân, đều, vuông)
- Hình bình hành có thể dùng làm hình biểu diễn cho các hình có tính chất của hình bình hành (vuông, thoi, chữ nhật,...)
- Một đường tròn được biểu diễn bởi một đường elip hoặc một đường tròn, hoặc đặc biệt có thể là một đoạn thẳng
Lời giải chi tiết
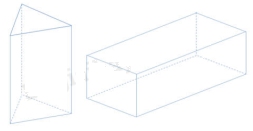
Bài 3 trang 119 SGK Toán 11 tập 1 - Cánh Diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài toán này yêu cầu học sinh phải nắm vững các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số.
Trước khi đi vào giải chi tiết, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Đề bài thường yêu cầu tìm đạo hàm của một hàm số, tìm cực trị của hàm số hoặc giải một phương trình liên quan đến đạo hàm.
Để giải Bài 3 trang 119 SGK Toán 11 tập 1 - Cánh Diều, chúng ta thực hiện theo các bước sau:
Giả sử hàm số cần xét là f(x) = x3 - 3x2 + 2. Ta thực hiện các bước sau:
Khi giải các bài toán về đạo hàm, cần chú ý các điểm sau:
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự sau:
Bài 3 trang 119 SGK Toán 11 tập 1 - Cánh Diều là một bài toán quan trọng giúp học sinh hiểu rõ hơn về ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và các lưu ý quan trọng trên, bạn sẽ tự tin hơn khi giải các bài toán tương tự.
| Hàm số | Đạo hàm | Điểm cực trị |
|---|---|---|
| f(x) = x3 - 3x2 + 2 | f'(x) = 3x2 - 6x | x = 0, x = 2 |