Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho Bài 1 trang 31 SGK Toán 11 tập 1 - Cánh diều. Chúng tôi hiểu rằng việc học Toán có thể gặp nhiều khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tốt nhất để giúp bạn nắm vững kiến thức.
Bài viết này sẽ cung cấp đáp án, phương pháp giải và những lưu ý quan trọng để bạn có thể tự tin giải quyết bài tập này. Hãy cùng bắt đầu!
Dùng đồ thị hàm số, tìm giá trị của x trên đoạn (left[ { - 2pi ;2pi } right]) để:
Đề bài
Dùng đồ thị hàm số, tìm giá trị của x trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\) để:
a) Hàm số y = sinx nhận giá trị bằng 1
b) Hàm số y = sinx nhận giá trị bằng 0
c) Hàm số y = cosx nhận giá trị bằng – 1
d) Hàm số y = cosx nhận giá trị bằng 0
Phương pháp giải - Xem chi tiết
Sử dụng đồ thị hàm số.
Lời giải chi tiết
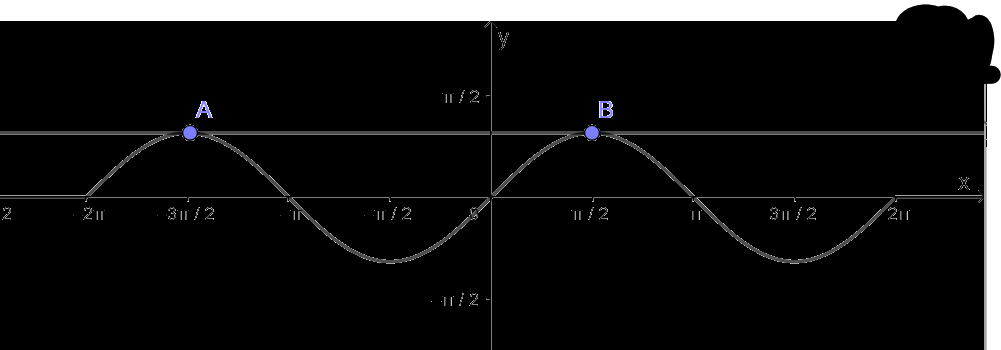
a) Hàm số y = sinx nhận giá trị bằng 1
- Vẽ hàm số y = sinx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 1
- Lấy giao điểm của hai hàm số y = sinx và y = 1 là A, B,...
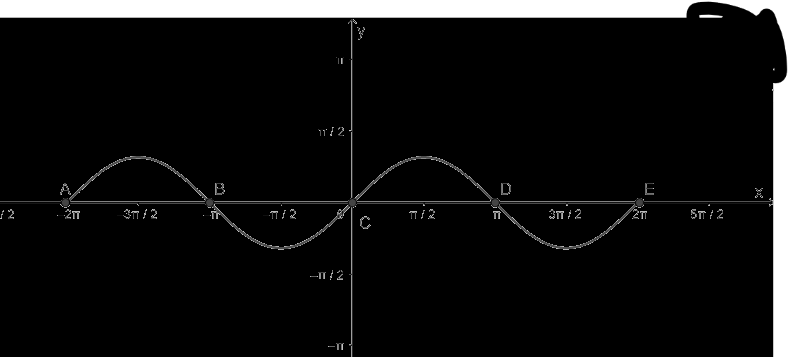
b) Hàm số y = sinx nhận giá trị bằng 0
- Vẽ hàm số y = sinx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = sinx và y = 0 là A, B, C, D, E,...
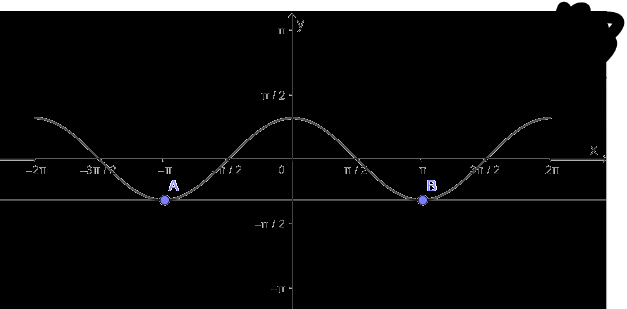
c) Hàm số y = cosx nhận giá trị bằng – 1
- Vẽ hàm số y = cosx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = - 1
- Lấy giao điểm của hai hàm số y = cosx và y = - 1 là A, B,...
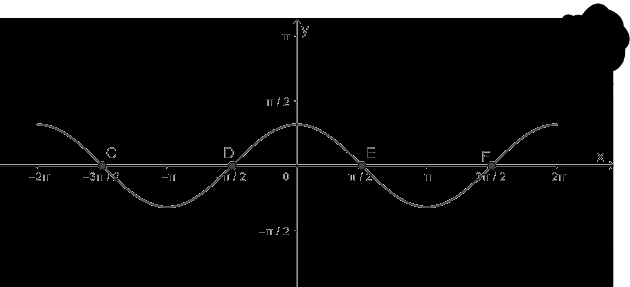
d) Hàm số y = cosx nhận giá trị bằng 0
- Vẽ hàm số y = cosx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = cosx và y = 0 là C, D, E, F,...
Bài 1 trang 31 SGK Toán 11 tập 1 - Cánh diều thuộc chương trình học Toán 11, tập trung vào việc ôn tập chương 1: Hàm số và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai, điều kiện xác định của hàm số, và cách xác định tập giá trị của hàm số.
Bài 1 yêu cầu học sinh xét hàm số f(x) = x2 - 4x + 3 và thực hiện các yêu cầu sau:
1. Xác định tập xác định của hàm số:
Hàm số f(x) = x2 - 4x + 3 là một hàm số bậc hai. Tập xác định của hàm số bậc hai là tập số thực, tức là D = ℝ.
2. Tìm tập giá trị của hàm số:
Hàm số f(x) = x2 - 4x + 3 có dạng f(x) = ax2 + bx + c, với a = 1, b = -4, c = 3. Vì a > 0, hàm số có parabol quay lên trên. Đỉnh của parabol có hoành độ x0 = -b / 2a = -(-4) / (2 * 1) = 2.
Tung độ của đỉnh là y0 = f(x0) = f(2) = 22 - 4 * 2 + 3 = 4 - 8 + 3 = -1.
Vì parabol quay lên trên, tập giá trị của hàm số là [y0; +∞) = [-1; +∞).
3. Vẽ đồ thị của hàm số:
Để vẽ đồ thị của hàm số, ta cần xác định một số điểm thuộc đồ thị. Ta có thể chọn các điểm có hoành độ x = 0, x = 1, x = 2, x = 3, x = 4.
Vẽ parabol đi qua các điểm (0; 3), (1; 0), (2; -1), (3; 0), (4; 3).
4. Xác định khoảng đồng biến, nghịch biến của hàm số:
Hàm số f(x) = x2 - 4x + 3 đồng biến trên khoảng (2; +∞) và nghịch biến trên khoảng (-∞; 2).
Bài 1 trang 31 SGK Toán 11 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, bạn sẽ tự tin hơn khi giải các bài tập tương tự.
Hãy tiếp tục luyện tập và khám phá thêm nhiều kiến thức Toán học thú vị tại giaitoan.edu.vn!