Chào mừng bạn đến với bài giải Bài 1 trang 25 SGK Toán 11 tập 2 – Cánh Diều tại giaitoan.edu.vn. Bài viết này cung cấp lời giải chi tiết, từng bước, giúp bạn hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ bạn học toán hiệu quả và đạt kết quả tốt nhất.
Người ta tiến hành phỏng vấn 40 người về một mẫu áo sơ mi mới. Người điều tra yêu cầu cho điểm mẫu áo đó theo thang điểm là 100.
Đề bài
Người ta tiến hành phỏng vấn 40 người về một mẫu áo sơ mi mới. Người điều tra yêu cầu cho điểm mẫu áo đó theo thang điểm là 100. Kết quả được trình bày trong Bảng 16.
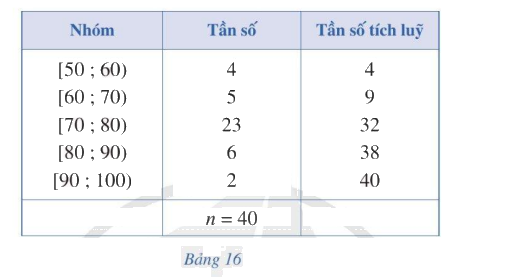
a) Trung vị của mẫu số liệu ghép nhóm trên gần nhất với giá trị:
A. 74
B. 75
C. 76
D. 77
b, Tứ phân vị của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng đơn vị) là:
A. \({Q_1} \approx 71;{Q_2} \approx 76;{Q_3} \approx 78\)
B. \({Q_1} \approx 71;{Q_2} \approx 75;{Q_3} \approx 78\)
C. \({Q_1} \approx 70;{Q_2} \approx 76;{Q_3} \approx 79\)
D. \({Q_1} \approx 70;{Q_2} \approx 75;{Q_3} \approx 79\)
c, Mốt của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng đơn vị) là:
A. 73
B. 74
C. 75
D. 76
Phương pháp giải - Xem chi tiết
a, Áp dụng công thức trung vị để làm.
b, Áp dụng công thức tứ phân vị để làm.
c, Áp dụng công thức tứ phân vị để làm.
Lời giải chi tiết
a,
Trung vị: \({M_e} = r + \left( {\frac{{\frac{n}{2} - c{f_{k - 1}}}}{{{n_k}}}} \right).d = 70 + \left( {\frac{{20 - 9}}{{23}}} \right).10 = \frac{{1720}}{{23}} \approx 74,8\)
⇨ Chọn: B. 75
b,
- Tứ phân vị thứ hai \({Q_2} = {M_e} = 75\) => Loại A, C
- Tứ phân vị thứ nhất: \({Q_1} = s + \left( {\frac{{\frac{n}{4} - c{f_{p - 1}}}}{{{n_p}}}} \right).h = 70 + \left( {\frac{{10 - 9}}{{23}}} \right).10 = \frac{{1620}}{{23}} \approx 70\)
⇨ Chọn D
c,
\({M_o} = u + \left( {\frac{{{n_i} - {n_{i - 1}}}}{{2{n_i} - {n_{i - 1}} - {n_{i + 1}}}}} \right).g = 70 + \left( {\frac{{23 - 5}}{{2.23 - 5 - 6}}} \right).10 = \frac{{526}}{7} \approx 75\)
⇨ Chọn C
Bài 1 trang 25 SGK Toán 11 tập 2 – Cánh Diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về hàm số và đồ thị để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh nắm vững các khái niệm về tập xác định, tập giá trị, tính đơn điệu và cực trị của hàm số.
Bài 1 thường bao gồm các dạng bài tập sau:
Để giải quyết bài tập này một cách hiệu quả, bạn cần:
(Ở đây sẽ là lời giải chi tiết cho từng câu hỏi của Bài 1, bao gồm các bước giải, giải thích và kết luận. Ví dụ:)
Câu a: Tìm tập xác định của hàm số y = √(2x - 1).
Để hàm số xác định, điều kiện là 2x - 1 ≥ 0, suy ra x ≥ 1/2. Vậy tập xác định của hàm số là D = [1/2, +∞).
Câu b: Tìm tập giá trị của hàm số y = x2 - 4x + 3.
Hàm số là một parabol có hệ số a = 1 > 0, nên có giá trị nhỏ nhất tại đỉnh. Hoành độ đỉnh là x = -b/2a = 2. Tung độ đỉnh là y = 22 - 4*2 + 3 = -1. Vậy tập giá trị của hàm số là [ -1, +∞).
Để hiểu rõ hơn về cách giải bài tập này, chúng ta hãy xem xét một ví dụ minh họa:
(Ví dụ về một bài tập tương tự và lời giải chi tiết)
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, bạn có thể tham khảo thêm các bài tập tương tự trong SGK Toán 11 tập 2 – Cánh Diều và các tài liệu tham khảo khác.
Bài 1 trang 25 SGK Toán 11 tập 2 – Cánh Diều là một bài tập quan trọng giúp bạn nắm vững kiến thức về hàm số và đồ thị. Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả mà chúng tôi cung cấp, bạn sẽ tự tin hơn khi giải quyết các bài tập tương tự.
| Khái niệm | Định nghĩa |
|---|---|
| Tập xác định | Tập hợp tất cả các giá trị của x sao cho hàm số có nghĩa. |
| Tập giá trị | Tập hợp tất cả các giá trị của y mà hàm số có thể nhận được. |
| Tính đơn điệu | Hàm số được gọi là đơn điệu nếu nó luôn tăng hoặc luôn giảm trên một khoảng nào đó. |
Chúc bạn học tập tốt!